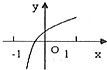已知a、b、c是△ABC的三边长,且满足
=0,则△ABC一定是( )
|
| A、等腰非等边三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
若函数f(x)=x3-ax2+4在区间[0,2]内单调递减,则( )
| A、a≥3 | B、a=3 |
| C、a≤3 | D、0<a<3 |
已知斜率为-
的直线l交椭圆C:
+
=1(a>b>0)于A,B两点,若点P(2,1)是AB的中点,则C的离心率等于( )
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)满足f(x+2)=f(x-2),y=f(x-2)关于y轴对称,当x∈(0,2)时,f(x)=log2x2,则下列结论中正确的是( )
| A、f(4.5)<f(7)<f(6.5) |
| B、f(7)<f(4.5)<f(6.5) |
| C、f(7)<f(6.5)<f(4.5) |
| D、f(4.5)<f(6.5)<f(7) |
在极坐标系中,圆C过极点,且圆心的极坐标是(a,
)(a>0),则圆C的极坐标方程是( )
| π |
| 2 |
| A、ρ=-2asinθ |
| B、ρ=2asinθ |
| C、ρ=-2acosθ |
| D、ρ=2acosθ |
函数y=
的单调递减区间是( )
| lnx |
| x |
| A、(e-1,+∞) |
| B、(0,e-1) |
| C、(-∞,e-1) |
| D、(e,+∞) |
设点P是椭圆
+
=1上的动点,F1为椭圆的左焦点,M(6,4)为定点,则|PM|+|PF1|的最大值是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、15 | ||
B、8+
| ||
| C、10 | ||
D、4
|
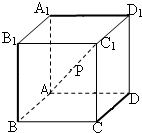 在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )
在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )| A、1个 | B、2个 |
| C、3个 | D、无穷多个 |
已知直线AB与抛物线y2=2x交于A,B两点,M是AB的中点,C是抛物线上的点,且使得
•
取最小值,抛物线在点C处的切线为l,则( )
| CA |
| CB |
| A、CM⊥AB | ||
| B、CM⊥l | ||
| C、CA⊥CB | ||
D、CM=
|
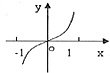
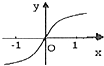
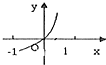
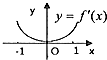 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )
已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )