题目内容

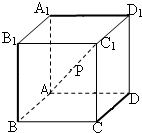在正方体AC1中，若点P在对角线AC1上，且P点到三条棱CD、A1D1、BB1的距离都相等，则这样的点共有（　　）
A、1个B、2个
C、3个D、无穷多个
考点：棱柱的结构特征
专题：空间位置关系与距离,立体几何
分析：根据正方体的特点，以及对角线AC1和三条棱CD、A1D1、BB1的位置关系，利用对称性即可得知对角线上的任何一个点都满足．
解答： 解：因为：CD、A1D1、BB1和对角线AC1的位置关系是一样，根据对称性，对角线AC1上的点都满足条件，可知有无穷多个．
故选：D．
点评：本题主要考查了正方体的结构特征，关键是了解直线的位置关系，属于基础题．
练习册系列答案
相关题目
设z=
x-y，x≥2y
x
4
+
y
2
，x＜2y
，若-2≤x≤2，-2≤y≤2，则z的最小值是
 
．
设等差数列{an}、等比数列{bn}首项都是1，公差与公比都是2，则ab1+ab2+ab3+ab4+ab5=
 
．
已知数列{an}中，an+1=
an
3an+1
，a1=1，则a2014=
 
．
设数列{an}满足
a1=2
an=2+
2
an-1
，则a3=
 
．
已知斜率为-
1
2
的直线l交椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）于A，B两点，若点P（2，1）是AB的中点，则C的离心率等于（　　）
A、
1
2
B、
2
2
C、
3
4
D、
3
2
函数y=(
1
2
)x2+1(x∈[-1，2])的值域为（　　）
A、[
1
32
，
1
4
]
B、(0，
1
4
]
C、[
1
32
，
1
2
]
D、[
1
4
，
1
2
]
函数f（x）=x-
2
x
的零点所在的大致区间是（　　）
A、（-4，-2）
B、（-2，-1）
C、（2，4）
D、（4，+∞）
若函数f（x）=asinx+bcosx（a，b∈R），非零向量
m
=（a，b），我们称
m
为函数f（x）的“相伴向量”，f（x）为向量
m
的“相伴函数”．
（Ⅰ）已知函数f（x）=（sinωx+cosωx）2+2cos2ωx-2（ω＞0）的最小正周期为2π，求函数f（x）的“相伴向量”；
（Ⅱ）记向量
n
=（
3
，1）的“相伴函数”为g（x），将g（x）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象上所有点向左平移
2π
3
个单位长度，得到函数h（x），若h（2α+
π
3
）=
6
5
，α∈（0，
π
2
），求sinα的值；
（Ⅲ）对于函数φ（x）=sinxcos2x，是否存在“相伴向量”？若存在，求出φ（x）“相伴向量”；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网