题目内容
已知斜率为-
的直线l交椭圆C:
+
=1(a>b>0)于A,B两点,若点P(2,1)是AB的中点,则C的离心率等于( )
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用点差法,结合点P(2,1)是AB的中点,斜率为-
,即可求出椭圆C的离心率.
| 1 |
| 2 |
解答:
解:设A(x1,y1),B(x2,y2),则
+
=1,
+
=1,
∵斜率为-
的直线l交椭圆C:
+
=1(a>b>0)于A,B两点,若点P(2,1)是AB的中点,
∴两式相减可得
+(-
)•
=0,
∴a=2b,
∴c=
b,
∴e=
=
.
故选:D.
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
∵斜率为-
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴两式相减可得
| 4 |
| a2 |
| 1 |
| 2 |
| 2 |
| b2 |
∴a=2b,
∴c=
| 3 |
∴e=
| c |
| a |
| ||
| 2 |
故选:D.
点评:本题考查椭圆C的离心率,考查学生的计算能力,正确运用点差法是关键.

练习册系列答案
相关题目
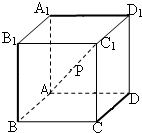 在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )
在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )| A、1个 | B、2个 |
| C、3个 | D、无穷多个 |
设正六边形ABCDEF的中心为点O,P为平面内任意一点,则
+
+
+
+
+
=( )
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
A、
| ||
B、
| ||
C、3
| ||
D、6
|
已知l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题为真命题的是( )
| A、若l⊥m,l⊥n,m?α,n?α,则l⊥α |
| B、若l⊥α,α∥β,m?β,则l⊥m |
| C、若l∥m,m?α,则l∥α |
| D、若l⊥α,α⊥β,m?β,则l∥m |
 如图,AB是⊙O的直径,PB,PC分别切⊙O于B,C,若∠ACE=38°,则∠P=
如图,AB是⊙O的直径,PB,PC分别切⊙O于B,C,若∠ACE=38°,则∠P=