题目内容
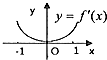 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )
已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )A、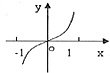 |
B、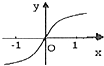 |
C、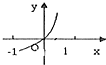 |
D、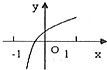 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:根据导数的图象,利用函数的单调性和导数的关系,得出所选的选项.
解答:
解:由导函数的图象可得,导函数f′(x)的值在(-∞,0]上的逐渐减小;
设(x0,f(x0))是f(x)图象上的动点,
则f′(x0)逐渐减小,即在点(x0,f(x0))处的切线斜率逐渐减小;
故函数f(x)在(-∞,0]上增长速度逐渐减小,故函数f(x)的图象是上凸型的.
同样的道理,导函数f′(x)的值在(0,+∞)上的逐渐增大,
故函数f(x)在(0,+∞)上增长速度逐渐变大,图象是下凹型的,故选A.
设(x0,f(x0))是f(x)图象上的动点,
则f′(x0)逐渐减小,即在点(x0,f(x0))处的切线斜率逐渐减小;
故函数f(x)在(-∞,0]上增长速度逐渐减小,故函数f(x)的图象是上凸型的.
同样的道理,导函数f′(x)的值在(0,+∞)上的逐渐增大,
故函数f(x)在(0,+∞)上增长速度逐渐变大,图象是下凹型的,故选A.
点评:本题主要考查函数的单调性和导数的关系.

练习册系列答案
相关题目
设点P是椭圆
+
=1上的动点,F1为椭圆的左焦点,M(6,4)为定点,则|PM|+|PF1|的最大值是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、15 | ||
B、8+
| ||
| C、10 | ||
D、4
|
定义在R上的函数f(x)满足f(x+2)=f(x)+1,且x∈[0,1]时,f(x)=4x,x∈(1,2)时,f(x)=
,令g(x)=2f(x)-x-4x∈[-6,2],则函数g(x)的零点个数为( )
| f(1) |
| x |
| A、9 | B、8 | C、7 | D、6 |
用二分法求方程3x+3x-8=0在区间(1,2)的过程中,设函数f(x)=3x+3x-8,算得f(1)<0,f(1.25)<0,f(1.5)>0,f(1.75)>0,则该方程的根属于( )
| A、(1,1.25) |
| B、(1.25,1.5) |
| C、(1.5,1.75) |
| D、(1.75,2) |
如果0<x<1,0<y<1,那么关于0<
<1( )
| x |
| y |
| A、正确 | B、错误 | C、不确定 |
 如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB⊥平面PAD,△PAD是正三角形,DC∥AB,DA=DC=2AB.
如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB⊥平面PAD,△PAD是正三角形,DC∥AB,DA=DC=2AB.