题目内容
已知函数f(x)满足f(x+2)=f(x-2),y=f(x-2)关于y轴对称,当x∈(0,2)时,f(x)=log2x2,则下列结论中正确的是( )
| A、f(4.5)<f(7)<f(6.5) |
| B、f(7)<f(4.5)<f(6.5) |
| C、f(7)<f(6.5)<f(4.5) |
| D、f(4.5)<f(6.5)<f(7) |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:求解本题需要先把函数的性质研究清楚,由三个条件知函数周期为4,其对称轴方程为x=2,在区间[0,2]上是增函数,观察四个选项发现自变量都不在已知的单调区间内故应用相关的性质将其值用区间[0,2]上的函数值表示出,以方便利用单调性比较大小
解答:
解:∵f(x+2)=f(x-2),y=f(x-2)关于y轴对称,
∴f(x)是以4为周期的周期函数,其图象的对称轴为x=2,
∵当x∈(0,2)时,f(x)=log2x2,
∴f(x)在区间(0,2)是增函数;
∴f(4.5)=f(0.5),
f(7)=f(3)=f(2+1)=f(2-1)=f(1),
f(6.5)=f(2.5)=f(2+0.5)=f(2-0.5)=f(1.5),
∵0<0.5<1<1.5<2,且函数y=f(x)在区间[0,2]上是增函数,
∴f(0.5)<f(1)<f(1.5),
即f(4.5)<f(7)<f(6.5),
故选:A.
∴f(x)是以4为周期的周期函数,其图象的对称轴为x=2,
∵当x∈(0,2)时,f(x)=log2x2,
∴f(x)在区间(0,2)是增函数;
∴f(4.5)=f(0.5),
f(7)=f(3)=f(2+1)=f(2-1)=f(1),
f(6.5)=f(2.5)=f(2+0.5)=f(2-0.5)=f(1.5),
∵0<0.5<1<1.5<2,且函数y=f(x)在区间[0,2]上是增函数,
∴f(0.5)<f(1)<f(1.5),
即f(4.5)<f(7)<f(6.5),
故选:A.
点评:本题综合考查了函数的周期性、函数的对称性与函数的单调性,涉及到了函数的三个主要性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知直线AB与抛物线y2=2x交于A,B两点,M是AB的中点,C是抛物线上的点,且使得
•
取最小值,抛物线在点C处的切线为l,则( )
| CA |
| CB |
| A、CM⊥AB | ||
| B、CM⊥l | ||
| C、CA⊥CB | ||
D、CM=
|
当0<x<1时,f(x)=
,则下列大小关系正确的是( )
| sinx |
| x |
| A、f2(x)<f(x)<f(x2) |
| B、f(x2)<f2(x)<f(x) |
| C、f(x)<f(x2)<f2(x) |
| D、f2(x)<f(x2)<f(x) |
函数f(x)=xsinx+cosx的导函数原点处的部分图象大致为( )
A、 |
B、 |
C、 |
D、 |
函数f(x)=x3-3x2+5的单调减区间是( )
| A、(0,2) |
| B、(0,3) |
| C、(0,1) |
| D、(0,5) |
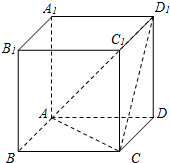 在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是
在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是