在四面体ABCD中,∠ABC=∠ABD=∠ADC=
,则下列是直角的为( )
| π |
| 2 |
| A、∠BCD | B、∠BDC |
| C、∠CBD | D、∠ACD |
已知向量
=(3,5,-1),
=(2,2,3),
=(1,-1,2),则向量
-
+4
的坐标为( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、(5,-1,4) |
| B、(5,1,-4) |
| C、(-5,1,4) |
| D、(-5,-1,4) |
若抛物线C1:y2=4x的焦点F恰好是双曲线C2:
-
=1(a>0,b>0)的右焦点,且C1与C2交点的连线过点F,则双曲线C2的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、2
| ||||||
C、3+2
| ||||||
D、
|
已知a是实数,(a+i)(1+i)是纯虚数,则a等于( )
| A、2 | B、1 | C、-1 | D、-2 |
已知函数y=f(x)的导函数y=f′(x)的图象如图,则( )
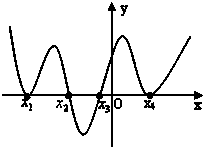

| A、函数f(x)有2个极大值点,2个极小值点 |
| B、函数f(x)有1个极大值点,1个极小值点 |
| C、函数f(x)有3个极大值点,1个极小值点 |
| D、函数f(x)有1个极大值点,3个极小值点. |
下列命题:
①直线l与平面α无数条直线平行,则l∥α;
②若直线m在平面α外,则m∥α;
③若直线m⊥n,直线n?α内,则m⊥α;
④若直线m∥n,m?α,直线n?β内,那么平面α∥平面β;
其中真命题的个数是为( )
①直线l与平面α无数条直线平行,则l∥α;
②若直线m在平面α外,则m∥α;
③若直线m⊥n,直线n?α内,则m⊥α;
④若直线m∥n,m?α,直线n?β内,那么平面α∥平面β;
其中真命题的个数是为( )
| A、0 | B、2 | C、3 | D、4 |
函数f(x)=
+
的定义域是( )
| x+3 |
| 1 |
| x+2 |
| A、{x|x≠2} |
| B、{x|x≥-3} |
| C、{x|x≥-3或x≠-2} |
| D、{x|x≥-3且x≠-2} |
对于函数f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“保三角形函数”.以下说法正确的是( )
| A、f(x)=1(x∈R)不是“保三角形函数” | ||
B、若定义在R上的函数f(x)的值域是[
| ||
C、f(x)=
| ||
| D、“保三角形函数”一定是单调函数 |
设f(x)是定义在R上的奇函数,且f(x+3)•f(x)=-1,f(-1)=2,则f(2008)=( )
| A、0.5 | B、0 | C、2 | D、-1 |