题目内容
设f（x）是定义在R上的奇函数，且f（x+3）•f（x）=-1，f（-1）=2，则f（2008）=（ ）
| A、0.5 | B、0 | C、2 | D、-1 |
考点：函数的值,函数奇偶性的性质,抽象函数及其应用
专题：计算题,函数的性质及应用
分析：f（x+6）=-
=f（x），f（x）是周期函数，周期为6，则有f（2008）=f（-2）=-f（2），令x=-1可得f（2）的值，代入可得答案．
| 1 |
| f(x+3) |
解答：
解：∵f（x+3）•f（x）=-1，f（-1）=2，
∴f（-1+3）•f（-1）=-1，f（2）=-
由 f（x+3）=-
，
可得：f（x+6）=-
=f（x），
∴f（x）是周期为6的周期函数，
∴f（2008）=f（6×334+4）=f（4）=f（-2）=-f（2）=
．
故选A．
∴f（-1+3）•f（-1）=-1，f（2）=-
| 1 |
| 2 |
| 1 |
| f(x) |
可得：f（x+6）=-
| 1 |
| f(x+3) |
∴f（x）是周期为6的周期函数，
∴f（2008）=f（6×334+4）=f（4）=f（-2）=-f（2）=
| 1 |
| 2 |
故选A．
点评：本题考查函数的周期性、奇偶性及运用，考查解决抽象函数的常用方法：赋值法，属于基础题．
练习册系列答案
相关题目
设函数f（x）=
在x=0处f（x）（ ）
|
| A、不连续 |
| B、连续，但不可导 |
| C、可导，但导数不连续 |
| D、可导，且导数连续 |
已知直线a和平面α，则能推出a∥α的是（ ）
| A、存在一条直线b，a∥b，且b∥α |
| B、存在一条直线b，a⊥b，且b⊥α |
| C、存在一个平面β，a?β，且α∥β |
| D、存在一个平面β，a∥β，且α∥β |
已知函数y=f（x）的导函数y=f′（x）的图象如图，则（ ）
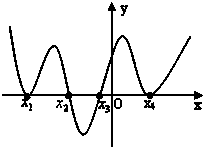
| A、函数f（x）有2个极大值点，2个极小值点 |
| B、函数f（x）有1个极大值点，1个极小值点 |
| C、函数f（x）有3个极大值点，1个极小值点 |
| D、函数f（x）有1个极大值点，3个极小值点． |
过双曲线
-
=1（a＞0，b＞0）的左焦点F（-c，0）作圆x2+y2=a2的切线，切点为E，延长FE交抛物线y2=4cx于点P，O为原点，若|FE|=|EP|，则双曲线离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|