题目内容
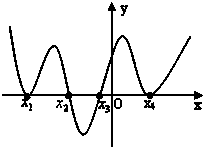
已知函数y=f（x）的导函数y=f′（x）的图象如图，则（ ）
| A、函数f（x）有2个极大值点，2个极小值点 |
| B、函数f（x）有1个极大值点，1个极小值点 |
| C、函数f（x）有3个极大值点，1个极小值点 |
| D、函数f（x）有1个极大值点，3个极小值点． |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：根据导函数的图象，确定函数的单调性，利用函数极值的定义即可得到结论．
解答：
解：由导数图象可知当x＜x2，或x＜x3时，f′（x）≥0，此时函数单调递增，
当x2＜x＜x3时，f′（x）＜0，此时函数单调递减，
∴当x=x2时，函数f（x）取得极大值，当x=x3时，函数f（x）取得极小值，
故极大值和极小值各为有一个，
故选：A
当x2＜x＜x3时，f′（x）＜0，此时函数单调递减，
∴当x=x2时，函数f（x）取得极大值，当x=x3时，函数f（x）取得极小值，
故极大值和极小值各为有一个，
故选：A
点评：本题主要考查函数极值的判断，根据导函数的图象判断函数的单调性时解决本题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
三次函数y=ax3-x在（-∞，+∞）内是减函数，则（ ）
| A、a≤0 | ||
| B、a=1 | ||
| C、a=2 | ||
D、a=
|
若x，y∈R，函数f（x）=（x+y）2+（
-y）2的最小值是（ ）
| 1 |
| x |
| A、4 | B、0 | C、2 | D、1 |
已知双曲线
-
=1（a＞0，b＞0），过其右焦点F且与渐近线y=-
x平行的直线分别与双曲线的右支和另一条渐近线交于A、B两点，且
=
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| FA |
| AB |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
设f（x）是定义在R上的奇函数，且f（x+3）•f（x）=-1，f（-1）=2，则f（2008）=（ ）
| A、0.5 | B、0 | C、2 | D、-1 |
抛物线y2=16x的准线过双曲线
-
=1的焦点，则k的值为（ ）
| x2 |
| 7 |
| y2 |
| k |
| A、3 | ||
| B、9 | ||
C、
| ||
D、
|
若不等式组
表示的平面区域经过四个象限，则实数λ的取值范围是（ ）
|
| A、（-∞，2） |
| B、[-1，1] |
| C、[-1，2） |
| D、（1，+∞） |