题目内容
对于函数f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“保三角形函数”.以下说法正确的是( )
| A、f(x)=1(x∈R)不是“保三角形函数” | ||
B、若定义在R上的函数f(x)的值域是[
| ||
C、f(x)=
| ||
| D、“保三角形函数”一定是单调函数 |
考点:进行简单的合情推理
专题:函数的性质及应用
分析:由题,根据“可构造三角形函数”的定义对四个选项进行判断即可得出正确选项
解答:
解:对于A选项,由题设所给的定义知,?a,b,c∈R,f(a),f(b),f(c)都是某一正三角形的三边长,是“可构造三角形函数”,故A选项错误;
对于B选项,由于
+
>e,可知,定义在R上的函数f(x)的值域是[
,e](e为自然对数的底数),则f(x)一定是“可构造三角形函数”,故B正确
对于C选项,当a=0,b=3,c=3时,f(a)=1>f(b)+f(c)=
,不构成三角形,故C错误;
对于D选项,由A选项判断过程知,D选项错误;
故选:B.
对于B选项,由于
| e |
| e |
| e |
对于C选项,当a=0,b=3,c=3时,f(a)=1>f(b)+f(c)=
| 1 |
| 5 |
对于D选项,由A选项判断过程知,D选项错误;
故选:B.
点评:本题考查综合法推理及函数的值域,三角形的性质,理解新定义是解答的关键

练习册系列答案
相关题目
函数f(x)=
+3(x>0)的最小值是( )
| x3+x |
| x2 |
| A、5 | |||
B、3
| |||
| C、3 | |||
| D、2 |
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案,在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,则下列哪个奖励模型比较符合该公司的要求( )
| A、y=0.25x | |||
| B、y=log7x+1 | |||
| C、y=1.002x | |||
D、y=
|
已知a是实数,(a+i)(1+i)是纯虚数,则a等于( )
| A、2 | B、1 | C、-1 | D、-2 |
已知x,y满足
,则z=2x+y的最小值是( )
|
| A、3 | ||
| B、-3 | ||
C、
| ||
| D、0 |
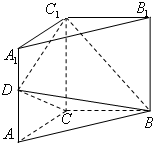 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=