正三棱锥的高为1，底面边长为2
3
，内有一个球与四个面都相切，则棱锥的内切球的半径为（　　）
A、
5
2
B、
3
-1
C、
1
2
D、
2
-1
已知函数y=
1
x-a
在（-∞，-1）上为减函数，则a的范围为（　　）
A、（-∞，-1）
B、（-1，+∞）
C、[-1，+∞）
D、（-∞，-1]
已知数列{an}为等比数列，且a2=2，a5=16，则公比q（　　）
A、1B、2C、4D、8
若0＜x＜y＜1，则（　　）
A、3y＜3x
B、(
1
4
)x＜(
1
4
)y
C、logx3＜logy3
D、x-
3
2
＞y-
3
2
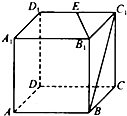如图，在正方体ABCD-A1B1C1D1中，棱长AB=2，点E是棱C1D1的中点，则异面直线B1E和BC1所成角的余弦值为（　　）
A、
15
5
B、
10
5
C、
15
10
D、
10
10
若sinαtanα＜0，且
cosα
tanα
＜0，则角α是（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知点P是双曲线
x2
4
-
y2
12
=1上一点，M，N是双曲线的左，右顶点，若直线PM的斜率的取值范围是[2，3]，则直线PN的斜率的取值范围是（　　）
A、[1，
3
2
]
B、[
3
2
，2]
C、[
3
2
，
5
2
]
D、[2，
5
2
]
某报社做了一次关于“什么是新时代的雷锋精神”的调查，在A，B，C，D四个单位回收的问卷数依次成等差数列，且共回收1 000份，因报道需要，再从回收的问卷中按单位分层抽取容量为150的样本，若在B单位抽取30份，则在D单位抽取的问卷份（　　）
A、60B、200
C、400D、140
已知函数f（x）=
-x2+2x，x≤0
ln(x+1)，x＞0
，若f（x）=ax有且只有一个实数解，则a的取值范围是（　　）
A、[1，2]
B、（-∞，0]
C、（-∞，0]∪[1，2]
D、（-∞，2]
已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ≤2π）若ω在集合{2，3，4}中任取一个数，φ在，{
1
3
π，
1
2
π，
2
3
π，π}中任取一个数，从这些函数中任意抽取两个，其图象能经过相同的平移后得到y=2sinωx的概率为（　　）
A、
5
36
B、
2
33
C、
5
66
D、
1
11
 0  207329  207337  207343  207347  207353  207355  207359  207365  207367  207373  207379  207383  207385  207389  207395  207397  207403  207407  207409  207413  207415  207419  207421  207423  207424  207425  207427  207428  207429  207431  207433  207437  207439  207443  207445  207449  207455  207457  207463  207467  207469  207473  207479  207485  207487  207493  207497  207499  207505  207509  207515  207523  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网