题目内容
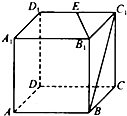如图，在正方体ABCD-A1B1C1D1中，棱长AB=2，点E是棱C1D1的中点，则异面直线B1E和BC1所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：异面直线及其所成的角
专题：
分析：在正方体ABCD-A1B1C1D1中，要求异面直线B1E和BC1所成角的余弦值，可通过作B1E平行线BF，即求BF和BC1所成角的余弦值，进一步利用余弦定理解△BFC1求得结果
解答：
解：
在正方体ABCD-A1B1C1D1中，棱长AB=2，点E是棱C1D1的中点，取CD的中点F，连接BF、FC1、EF
根据正方体的性质 B1E∥BF
∵棱长AB=2
∴进一步求得BF=
FC1=
BC1=2
∴在△BFC1中，利用余弦定理：cos∠BFC1=
∵BF=
FC1=
BC1=2
∴cos∠BFC1=
即为B1E和BC1所成角的余弦值
故答案为：B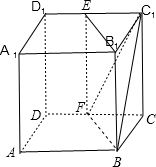
在正方体ABCD-A1B1C1D1中，棱长AB=2，点E是棱C1D1的中点，取CD的中点F，连接BF、FC1、EF
根据正方体的性质 B1E∥BF
∵棱长AB=2
∴进一步求得BF=
| 5 |
| 5 |
| 2 |
∴在△BFC1中，利用余弦定理：cos∠BFC1=
| BF2+BC12-FC12 |
| 2BF•BC1 |
∵BF=
| 5 |
| 5 |
| 2 |
∴cos∠BFC1=
| ||
| 5 |
即为B1E和BC1所成角的余弦值
故答案为：B
点评：本题重点考查异面直线所成角，可以通过中点得到平行线，把空间问题平面转化为平面问题，进一步通过利用余弦定理解三角形得到结果．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如图，由抛物线C1：y2=4x与C2：y2=8（3-x）围成一个封闭图形OACB，F是抛物线的焦点，直线y=h（h＜2）交两弧于P、Q两点，则当h=5人并排一起照相，甲恰好坐在中间的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
的定义域是（ ）
log
|
| A、（-∞，4） |
| B、（-∞，4] |
| C、（3，4] |
| D、（3，4） |
已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ≤2π）若ω在集合{2，3，4}中任取一个数，φ在，{
π，
π，
π，π}中任取一个数，从这些函数中任意抽取两个，其图象能经过相同的平移后得到y=2sinωx的概率为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已sin（
-x）=
，则sin2x的值为（ ）
| π |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、±
|
复数
的值是（ ）
| 1+2i |
| 3+i3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式x2＜2x+3的解集是（ ）
| A、（-1，3） |
| B、（-1，1） |
| C、（-3，-1）∪（1，3） |
| D、（-3，3） |