题目内容
已知函数f(x)=
,若f(x)=ax有且只有一个实数解,则a的取值范围是( )
|
| A、[1,2] |
| B、(-∞,0] |
| C、(-∞,0]∪[1,2] |
| D、(-∞,2] |
考点:分段函数的应用,根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:分别求出x≤0和x>0时函数y=f(x)-ax零点的取值情况,利用数形结合切点和直线y=ax,a的取值范围即可得到.
解答:
 解:由y=f(x)-ax=0,得f(x)=ax
解:由y=f(x)-ax=0,得f(x)=ax
∵f(0)=0,
∴x=0是函数y=f(x)-ax的一个零点,
由条件可知只有一个零点,
故当x<0时,由f(x)=ax,
得-x2+2x=ax,
即-x+2=a,解得x=2-a,
由x=2-a≥0,解得a≤2;
当x>0时,函数f(x)=ln(x+1),
f'(x)=
∈(0,1),
∵x>0,
∴要使函数y=f(x)-ax在x>0时没有零点,
则a≥1或a≤0,
∵a≤2,
∴1≤a<2或a≤0,
即实数k的取值范围是[1,2]∪(-∞,0].
故选:C.
 解:由y=f(x)-ax=0,得f(x)=ax
解:由y=f(x)-ax=0,得f(x)=ax∵f(0)=0,
∴x=0是函数y=f(x)-ax的一个零点,
由条件可知只有一个零点,
故当x<0时,由f(x)=ax,
得-x2+2x=ax,
即-x+2=a,解得x=2-a,
由x=2-a≥0,解得a≤2;
当x>0时,函数f(x)=ln(x+1),
f'(x)=
| 1 |
| x+1 |
∵x>0,
∴要使函数y=f(x)-ax在x>0时没有零点,
则a≥1或a≤0,
∵a≤2,
∴1≤a<2或a≤0,
即实数k的取值范围是[1,2]∪(-∞,0].
故选:C.
点评:本题主要考查函数零点的个数的应用,利用方程和函数之间的关系,将函数零点转化为函数图象相交问题,利用数形结合是解决此类问题的关键,利用切线的临界位置是解决问题的突破点.

练习册系列答案
相关题目
下列给出的赋值语句中正确的是( )
| A、3=A | B、x=-x |
| C、B=A=2 | D、x+y=0 |
A、B是双曲线
-
=1右支上的两点,若弦AB的中点到Y轴的距离是4,则|AB|的最大值为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、2 | B、4 | C、6 | D、8 |
若0<x<y<1,则( )
| A、3y<3x | ||||
B、(
| ||||
| C、logx3<logy3 | ||||
D、x-
|
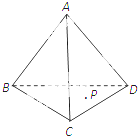 如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )
如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )| A、4个 | B、6个 | C、8个 | D、14个 |
在抛物线y2=4x上恒有两点关于直线l:y=kx+3则对称,k的取值范围是( )
| A、-1<k<0 |
| B、0<k<1 |
| C、-1≤k≤0 |
| D、0≤k≤1 |
已知0<b<1,0<α<
,x=(sinα)logbsinα,y=(cosα)logbcosα,z=(sinα)logbcosα则三数的大小关系是( )
| π |
| 4 |
| A、x<y<z |
| B、z<x<y |
| C、x<z<y |
| D、y<z<x |



