题目内容
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ≤2π)若ω在集合{2,3,4}中任取一个数,φ在,{
π,
π,
π,π}中任取一个数,从这些函数中任意抽取两个,其图象能经过相同的平移后得到y=2sinωx的概率为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:确定从中任意抽取两个函数的方法数,再考虑向右平移相同个单位得到函数y=2sinωx的图象的方法数,利用古典概型的概率公式,即可求得结论.
解答:
解:这一组函数共有3×4=12个,从中任意抽取两个函数共有
=66种不同的方法.
其中从这些函数中任意抽取两个,向右平移个
单位得到函数y=2sinωx的图象有3种取法;
向右平移
个单位得到函数y=2sinωx的图象有2种取法;
向右平移
个单位得到函数y=2sinωx的图象有2种取法;
向右平移
个单位得到函数y=2sinωx的图象有1种取法;
向右平移
个单位得到函数y=2sinωx的图象也有1种取法,
向右平移
个单位得到函数y=2sinωx的图象也有1种取法,
向右平移
个单位得到函数y=2sinωx的图象也有1种取法,
向右平移
个单位得到函数y=2sinωx的图象也有1种取法,
则满足两个图象能经过相同的平移后得到y=2sinωx的取法共有:
+
+
=5种,
故其图象能经过相同的平移后得到y=2sinωx的概率P=
,
故选:C
| C | 2 12 |
其中从这些函数中任意抽取两个,向右平移个
| π |
| 6 |
向右平移
| π |
| 3 |
向右平移
| π |
| 4 |
向右平移
| π |
| 2 |
向右平移
| 2π |
| 9 |
向右平移
| π |
| 9 |
向右平移
| π |
| 8 |
向右平移
| π |
| 12 |
则满足两个图象能经过相同的平移后得到y=2sinωx的取法共有:
| C | 2 3 |
| C | 2 2 |
| C | 2 2 |
故其图象能经过相同的平移后得到y=2sinωx的概率P=
| 5 |
| 66 |
故选:C
点评:本题考查古典概型的概率,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
设
,
是夹角为
的单位向量,且
=2
+3
,
=k
-4
.若
⊥
,则实数k的值为( )
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
函数f(x)=|sinx|+
sinx(0≤x≤2π)与函数g(x)=a(a是常数)有两个不同的交点,则a的取值范围是( )
| 1 |
| 2 |
A、(0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
若cosα-3sinα=
,则tanα=( )
| 10 |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|
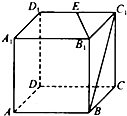 如图,在正方体ABCD-A1B1C1D1中,棱长AB=2,点E是棱C1D1的中点,则异面直线B1E和BC1所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,棱长AB=2,点E是棱C1D1的中点,则异面直线B1E和BC1所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△AB中,已知
•
=
•
,若|
+
|=2,且B∈[
,
],则
•
的取值范围为( )
| BC |
| CA |
| CA |
| AB |
| BA |
| BC |
| π |
| 3 |
| 2π |
| 3 |
| BA |
| BC |
A、[-2,
| ||
B、[-1,
| ||
C、[0,
| ||
D、[1,
|
已知椭圆
+
=1(a>b>0)的左顶点为E,过原点O的直线交椭圆于A,B两点,若|AB|=|BE|=2,cos∠ABE=
,则椭圆方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某单位有老年人28人,中年人44人,青年人72人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
| A、简单随机抽样 |
| B、系统抽样 |
| C、分层抽样 |
| D、先从老年人中剔除一人,然后分层抽样 |