已知平面向量
,
满足|
|=2,|
|=1,
与
夹角为60°,且2
-k
与
+
垂直,则实数k为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-5 | B、5 | C、4 | D、3 |
一元二次不等式2kx2+kx-
<0对一切实数x恒成立,则k的范围是( )
| 3 |
| 8 |
| A、(-3,0) |
| B、(-3,0] |
| C、(-∞,-3] |
| D、(0,+∞) |
已知函数①f(x)=5x2;②f(x)=5cosx;③f(x)=5ex;④f(x)=5lnx,其中对于f(x)定义域内的任意一个自变量x1,都存在唯一的自变量x2,使
=5成立的函数有( )个.
| f(x1)f(x2) |
| A、1个 | B、2个 | C、3个 | D、4个 |
设函数f(x)=lnx-ax+2.
(1)若a>0,求函数f(x)的单调区间和极值;
(2)若a>-e时,函数g(x)=ex-xf′(x)在[
,3]上有最大值e3,其中f′(x)的导数,求实数a的值.
(1)若a>0,求函数f(x)的单调区间和极值;
(2)若a>-e时,函数g(x)=ex-xf′(x)在[
| 1 |
| 2 |
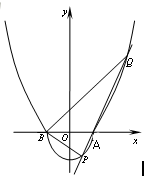 如图,由半椭圆x2+
如图,由半椭圆x2+