题目内容
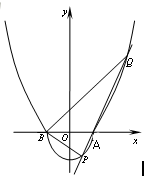 如图,由半椭圆x2+
如图,由半椭圆x2+| y2 |
| a |
| 1 |
| 2 |
| 3 |
(1)求a的值;
(2)设A(1,0),B(-1,0),过A且斜率为k的直线l与曲线C相交于P、A、Q三点,问是否存在实数k使得∠QBP=90°?若存在,求出k的值;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)把点(
,-
)代入半椭圆x2+
=1(y≤0,a>0),即可解出a.
(2)假设存在实数k使得∠QBP=90°.则直线l的方程为:y=k(x-1),设P(x1,y1),Q(x2,y2).
把直线l的方程分别与抛物线方程、椭圆方程联立可得P,Q的坐标(用k表示),再利用∠QBP=90°,可得
•
=0,即(x2+1,y2)•(x1+1,y1)=0,解出即可.
| 1 |
| 2 |
| 3 |
| y2 |
| a |
(2)假设存在实数k使得∠QBP=90°.则直线l的方程为:y=k(x-1),设P(x1,y1),Q(x2,y2).
把直线l的方程分别与抛物线方程、椭圆方程联立可得P,Q的坐标(用k表示),再利用∠QBP=90°,可得
| BQ |
| BP |
解答:
解:(1)把点(
,-
)代入半椭圆x2+
=1(y≤0,a>0),可得
+
=1.解得a=4.
(2)假设存在实数k使得∠QBP=90°.则直线l的方程为:y=k(x-1),设P(x1,y1),Q(x2,y2).
联立
,化为x2-kx+k-1=0,解得x2=k-1,y2=k2-2k,Q(k-1,k2-2k).
联立
,化为(4+k2)x2-2k2x+k2-4=0,解得x1=
,y1=
,
P(
,
).
∵∠QBP=90°,∴
•
=0,
∴(x2+1,y2)•(x1+1,y1)=0,
∴k•
+
=0,k≠0.
化为k=
.
经过验证满足条件.
因此存在实数k=
使得∠QBP=90°.
| 1 |
| 2 |
| 3 |
| y2 |
| a |
| 1 |
| 4 |
| 3 |
| a |
(2)假设存在实数k使得∠QBP=90°.则直线l的方程为:y=k(x-1),设P(x1,y1),Q(x2,y2).
联立
|
联立
|
| k2-4 |
| k2+4 |
| -8k |
| k2+4 |
P(
| k2-4 |
| k2+4 |
| -8k |
| k2+4 |
∵∠QBP=90°,∴
| BQ |
| BP |
∴(x2+1,y2)•(x1+1,y1)=0,
∴k•
| 2k2 |
| k2+4 |
| -8k(k2-2k) |
| k2+4 |
化为k=
| 8 |
| 3 |
经过验证满足条件.
因此存在实数k=
| 8 |
| 3 |
点评:本题考查了椭圆的标准方程、直线与椭圆抛物线相交问题转化为方程联立可得交点坐标、向量垂直与数量积的关系,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
设i是虚数单位,
(1+i)=3-i,则复数z=( )
| z |
| A、1-2i | B、1+2i |
| C、2-i | D、2+i |
已知函数①f(x)=5x2;②f(x)=5cosx;③f(x)=5ex;④f(x)=5lnx,其中对于f(x)定义域内的任意一个自变量x1,都存在唯一的自变量x2,使
=5成立的函数有( )个.
| f(x1)f(x2) |
| A、1个 | B、2个 | C、3个 | D、4个 |
边长为5cm的正方形EFGH是圆柱的轴截面,则从E点沿圆柱的侧面到相对顶点G的最短距离是( )
| A、10 | ||||
B、
| ||||
C、5
| ||||
D、5
|
 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC上的一点,若AF⊥BE,垂足为F,求证:∠BFD=∠C.
如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC上的一点,若AF⊥BE,垂足为F,求证:∠BFD=∠C.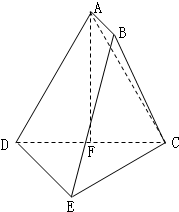 已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.