题目内容
已知a,b,c,d均为实数,函数f(x)=
x3+
x2+cx+d(a<0)有两个极值点x1,x2且x1<x2,满足f(x2)=x1,则方程af2(x)+bf(x)+c=0的实根的个数是 .
| a |
| 3 |
| b |
| 2 |
考点:利用导数研究函数的极值,根的存在性及根的个数判断
专题:计算题,数形结合,导数的综合应用
分析:求导数f′(x),由题意知x1,x2是方程ax2+bx+c=0的两根,从而关于f(x)的方程a(f(x))2+bf(x)+c=0有两个根,作出草图,由图象可得答案.
解答:
 解:∵f(x)=
解:∵f(x)=
x3+
x2+cx+d(a<0)
∴f′(x)=ax2+bx+c,
由题意知x1,x2是方程ax2+bx+c=0的两根,即x1,x2是函数的两个极值点,
不妨设x2>x1,从而关于f(x)的方程a[f(x)]2+b[f(x)]+c=0有两个根,
所以f(x)=x1,或f(x)=x2根据题意画图,
所以f(x)=x1有两个不等实根,f(x)=x2只有一个不等实根,
综上方程a[f(x)]2+bf(x)+c=0的不同实根个数为3个.
故答案为:3.
 解:∵f(x)=
解:∵f(x)=| a |
| 3 |
| b |
| 2 |
∴f′(x)=ax2+bx+c,
由题意知x1,x2是方程ax2+bx+c=0的两根,即x1,x2是函数的两个极值点,
不妨设x2>x1,从而关于f(x)的方程a[f(x)]2+b[f(x)]+c=0有两个根,
所以f(x)=x1,或f(x)=x2根据题意画图,
所以f(x)=x1有两个不等实根,f(x)=x2只有一个不等实根,
综上方程a[f(x)]2+bf(x)+c=0的不同实根个数为3个.
故答案为:3.
点评:考查函数零点的概念、以及对嵌套型函数的理解,考查数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=sin(
-2x)×sin(
+2x),则f(x)的最小正周期是( )
| π |
| 4 |
| π |
| 4 |
A、
| ||
| B、π | ||
| C、2π | ||
D、
|
一元二次不等式2kx2+kx-
<0对一切实数x恒成立,则k的范围是( )
| 3 |
| 8 |
| A、(-3,0) |
| B、(-3,0] |
| C、(-∞,-3] |
| D、(0,+∞) |
 正三棱锥D-ABC中,底面三角形ABC的面积为4
正三棱锥D-ABC中,底面三角形ABC的面积为4| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、与EF位置有关,总面积不确定 |
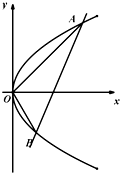 如图,已知抛物线y2=2px(p>0)上点(2,a)到焦点F的距离为3,直线l:my=x+t(t≠0)交抛物线C于A,B两点,且满足OA⊥OB.圆E是以(-p,p)为圆心,p为直径的圆.
如图,已知抛物线y2=2px(p>0)上点(2,a)到焦点F的距离为3,直线l:my=x+t(t≠0)交抛物线C于A,B两点,且满足OA⊥OB.圆E是以(-p,p)为圆心,p为直径的圆.