题目内容
已知函数①f(x)=5x2;②f(x)=5cosx;③f(x)=5ex;④f(x)=5lnx,其中对于f(x)定义域内的任意一个自变量x1,都存在唯一的自变量x2,使
=5成立的函数有( )个.
| f(x1)f(x2) |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:验证f(x)定义域内的任意一个自变量x1,都存在唯一的自变量x2,f(x2)=
,即看f(x1)\的倒数的25倍是否唯一.
对于①,对于定义域内的任意一个非零实数x,都有倒数,但倒数对应的自变量x2有两个,不唯一,故不满足条件. 通过举反例可得②④不正确.对于③,对定义域内的任意一个自变量,函数都有唯一的倒数,故满足条件.
| 25 |
| f(x1) |
对于①,对于定义域内的任意一个非零实数x,都有倒数,但倒数对应的自变量x2有两个,不唯一,故不满足条件. 通过举反例可得②④不正确.对于③,对定义域内的任意一个自变量,函数都有唯一的倒数,故满足条件.
解答:
解:对于①f(x)=5x2,对于定义域内的任意一个非零实数x,都有倒数,但倒数对应的自变量x2,有两个,它们互为相反数,故不满足条件.
对于②f(x)=5cosx,当x=2kπ+
时,函数值f(x)=0,函数没有倒数,故不满足条件.
对于③f(x)=5ex ,对任意一个自变量,函数都有唯一的倒数,故满足条件.
对于④f(x)=5lnx,x=1时,lnx没有倒数,故不满足条件.
故选A.
对于②f(x)=5cosx,当x=2kπ+
| π |
| 2 |
对于③f(x)=5ex ,对任意一个自变量,函数都有唯一的倒数,故满足条件.
对于④f(x)=5lnx,x=1时,lnx没有倒数,故不满足条件.
故选A.
点评:本题是选择题,主要考查函数的概念及其构成要素,可采用逐一检验的方法进行判定,注意抓住两个关键词“任意”与“唯一”进行判定,属于基础题.

练习册系列答案
相关题目
已知椭圆C1:
+
=1(a>b>0)与圆C2:x2+y2=b2,若在椭圆C1上不存在点P,使得由点P所作的圆C2的两条切线互相垂直,则椭圆C1的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
设y1=0.3
,y2=0.4
,y3=0.4
( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| A、y3<y2<y1 |
| B、y1<y2<y3 |
| C、y2<y3<y1 |
| D、y1<y3<y2 |
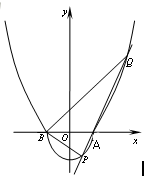 如图,由半椭圆x2+
如图,由半椭圆x2+