题目内容
一元二次不等式2kx2+kx-
＜0对一切实数x恒成立，则k的范围是（ ）
| 3 |
| 8 |
| A、（-3，0） |
| B、（-3，0] |
| C、（-∞，-3] |
| D、（0，+∞） |
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：当k=0，有-
＜0恒成立；当k≠0，令y=2kx2+kx-
，由y＜0对一切实数x恒成立，可知抛物线开口向下，且与x轴没公共点，故k＜0，且△＜0．
| 3 |
| 8 |
| 3 |
| 8 |
解答：
解：当k=0，有-
＜0恒成立；
当k≠0，令y=2kx2+kx-
∵y＜0对一切实数x恒成立，
∴开口向下，抛物线与x轴没公共点，
即k＜0，且△=k2+3k＜0，
解得-3＜k＜0；
综上所述，k的取值范围为-3＜k≤0．
故选：B
| 3 |
| 8 |
当k≠0，令y=2kx2+kx-
| 3 |
| 8 |
∵y＜0对一切实数x恒成立，
∴开口向下，抛物线与x轴没公共点，
即k＜0，且△=k2+3k＜0，
解得-3＜k＜0；
综上所述，k的取值范围为-3＜k≤0．
故选：B
点评：主要考查一元二次函数及一元二次不等式及其解法等考点的理解，属于基础题．
练习册系列答案
相关题目
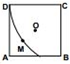
如图，△ADP为正三角形，O为正方形ABCD中心，而ADP⊥面ABCD，M为面ABCD内的点，且满足MP=MC．则点M在正方形ABCD内的轨迹为（ ）
如图平行四边形ABCD中，∠DAB=60°，AB=2AD=2，M为边CD的中点，沿BM将△CBM折起使得平面BMC⊥平面ABMD．