题目内容
已知函数f(x)=
,若命题“?t∈R,且t≠0,使得f(t)≥kt”是假命题,则实数k的取值范围是 .
|
考点:特称命题
专题:函数的性质及应用,不等式的解法及应用,简易逻辑
分析:由x<1时函数的单调性,画出函数f(x)的图象,把命题“存在t∈R,且t≠0,使得f(t)≥kt”是假命题转化为“任意t∈R,且t≠0,使得f(t)<kt恒成立”,
作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),求出切点和斜率,设直线与y=x(x-1)2(x≤0)图象相切于点(0,0),得切线斜率k=1,
由图象观察得出k的取值范围.
作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),求出切点和斜率,设直线与y=x(x-1)2(x≤0)图象相切于点(0,0),得切线斜率k=1,
由图象观察得出k的取值范围.
解答:
 解:当x<1时,f(x)=-|x3-2x2+x|=-|x(x-1)2|=
解:当x<1时,f(x)=-|x3-2x2+x|=-|x(x-1)2|=
,
当x<0,f′(x)=(x-1)(3x-1)>0,∴f(x)是增函数;
当0≤x<1,f′(x)=-(x-1)(3x-1),∴f(x)在区间(0,
)上是减函数,
在(
,1)上是增函数;
画出函数y=f(x)在R上的图象,如图所示;
命题“存在t∈R,且t≠0,使得f(t)≥kt“是假命题,
即为任意t∈R,且t≠0时,使得f(t)<kt恒成立;
作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),
则由(lnx)′=
,得k=
,
即lnm=km,解得m=e,k=
;
设直线与y=x(x-1)2(x≤0)的图象相切于点(0,0),
∴y′=[x(x-1)2]′=(x-1)(3x-1),则有k=1,
由图象可得,当直线绕着原点旋转时,转到与y=lnx(x≥1)图象相切,
以及与y=x(x-1)2(x≤0)图象相切时,直线恒在上方,即f(t)<kt恒成立,
∴k的取值范围是(
,1].
故答案为:(
,1].
 解:当x<1时,f(x)=-|x3-2x2+x|=-|x(x-1)2|=
解:当x<1时,f(x)=-|x3-2x2+x|=-|x(x-1)2|=
|
当x<0,f′(x)=(x-1)(3x-1)>0,∴f(x)是增函数;
当0≤x<1,f′(x)=-(x-1)(3x-1),∴f(x)在区间(0,
| 1 |
| 3 |
在(
| 1 |
| 3 |
画出函数y=f(x)在R上的图象,如图所示;
命题“存在t∈R,且t≠0,使得f(t)≥kt“是假命题,
即为任意t∈R,且t≠0时,使得f(t)<kt恒成立;
作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),
则由(lnx)′=
| 1 |
| x |
| 1 |
| m |
即lnm=km,解得m=e,k=
| 1 |
| e |
设直线与y=x(x-1)2(x≤0)的图象相切于点(0,0),
∴y′=[x(x-1)2]′=(x-1)(3x-1),则有k=1,
由图象可得,当直线绕着原点旋转时,转到与y=lnx(x≥1)图象相切,
以及与y=x(x-1)2(x≤0)图象相切时,直线恒在上方,即f(t)<kt恒成立,
∴k的取值范围是(
| 1 |
| e |
故答案为:(
| 1 |
| e |
点评:本题考查了分段函数的应用问题,也考查了存在性命题与全称性命题的互相转化问题以及不等式恒成立的问题,是较难的题目.

练习册系列答案
相关题目
下列函数中,满足“对任意的x1,x2∈R,当x1<x2时,都有f(x1)<f(x2)”的是( )
| A、y=log2x | ||
B、y=-
| ||
| C、y=2x | ||
| D、y=x2 |
在抛物线y2=8x中,以(1,-1)为中点的弦所在的直线方程为( )
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
已知平面向量
,
满足|
|=2,|
|=1,
与
夹角为60°,且2
-k
与
+
垂直,则实数k为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-5 | B、5 | C、4 | D、3 |
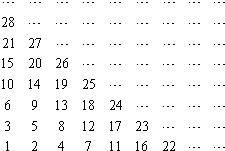 将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=
将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=