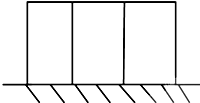
 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y(1)请把y表示成x的函数;
(2)当x为何值时,函数取最大值,并求出最大值.
已知等差数列{an}的首项a1≠0,前n项和是Sn,则
等于( )
| S5n |
| S3n-S2n |
| A、2 | B、4 | C、5 | D、9 |
 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y| S5n |
| S3n-S2n |
| A、2 | B、4 | C、5 | D、9 |