题目内容
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a3+a5+…+a2n-1.
(1)求{an}的通项公式;
(2)求a1+a3+a5+…+a2n-1.
考点:等差数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)设{an}的公差为d,由题意得a112=a1a13,代值解关于d的方程,可得通项公式;
(2)由(1)知a2n-1=-4n+29,易得{a2n-1}是首项为25,公差为-4的等差数列,由求和公式可得.
(2)由(1)知a2n-1=-4n+29,易得{a2n-1}是首项为25,公差为-4的等差数列,由求和公式可得.
解答:
解:(1)设{an}的公差为d,
由题意得a112=a1a13,
即(a1+10d)2=a1(a1+12d).
整理可得d(2a1+25d)=0.
又a1=25,∴d=0或d=-2.
∵等差数列{an}的公差不为零,∴d=-2
∴an=25-2(n-1)=-2n+27.
(2)令S=a1+a3+a5+…+a2n-1.
由(1)知a2n-1=-4n+29,
故{a2n-1}是首项为25,公差为-4的等差数列.
∴Sn=
(a1+a2n-1)=
(-4n+54)=-2n2+27n.
由题意得a112=a1a13,
即(a1+10d)2=a1(a1+12d).
整理可得d(2a1+25d)=0.
又a1=25,∴d=0或d=-2.
∵等差数列{an}的公差不为零,∴d=-2
∴an=25-2(n-1)=-2n+27.
(2)令S=a1+a3+a5+…+a2n-1.
由(1)知a2n-1=-4n+29,
故{a2n-1}是首项为25,公差为-4的等差数列.
∴Sn=
| n |
| 2 |
| n |
| 2 |
点评:本题考查等差数列的前n项和,属基础题.

练习册系列答案
相关题目
已知向量
=(1,-n),
=(2,n),若
•
=1,则实数n=( )
| a |
| b |
| a |
| b |
| A、1或-1 | B、-1 | C、0 | D、-2 |
已知函数f(x)=|x+2|+1,g(x)=ax.若关于x的方程f(x)=g(x)有两个不相等的实根,则实数a的取值范围是( )
A、(-1,-
| ||
B、(
| ||
C、(0,
| ||
| D、(-∞,-1) |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y,则sinx≠siny”的逆否命题为假命题 |
| D、命题“若x2+y2≠0,则x、y不全为零”的否命题为真命题 |
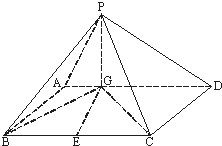 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=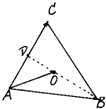 (1)设x,y∈R,向量
(1)设x,y∈R,向量