题目内容
设Sn为数列{an}的前n项之和,若不等式n2an2+4Sn2≥λn2a12对任何等差数列{an}及任何正整数n恒成立,则λ的最大值为 .
考点:数列的求和
专题:等差数列与等比数列
分析:由于不等式n2an2+4Sn2≥λn2a12对任何等差数列{an}及任何正整数n恒成立,利用等差数列的前n项和公式可得n2
+n2(a1+an)2≥λn2
,当a1≠0时,化为λ≤2(
+
)2+
,利用二次函数的单调性即可得出.
| a | 2 n |
| a | 2 1 |
| an |
| a1 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵不等式n2an2+4Sn2≥λn2a12对任何等差数列{an}及任何正整数n恒成立,
Sn=
,
∴n2
+n2(a1+an)2≥λn2
,
当a1≠0时,化为λ≤2(
)2+2
+1=2(
+
)2+
,
当
=-
时,上式等号成立.
∴λ≤
.
故答案为:
.
Sn=
| n(a1+an) |
| 2 |
∴n2
| a | 2 n |
| a | 2 1 |
当a1≠0时,化为λ≤2(
| an |
| a1 |
| an |
| a1 |
| an |
| a1 |
| 1 |
| 2 |
| 1 |
| 2 |
当
| an |
| a1 |
| 1 |
| 2 |
∴λ≤
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了等差数列的通项公式与前n项和公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设
、
、
是任意的非零平面向量,且相互不共线,则
①(
•
)
=(
•
)
;
②|
|-|
|>|
-
|;
③(
•
)
-(
•
)
与
垂直;
④(3
+2
)•(3
-2
)=9|
|2-4|
|2中,是真命题的有( )
| a |
| b |
| c |
①(
| a |
| b |
| c |
| c |
| a |
| b |
②|
| a |
| b |
| a |
| b |
③(
| b |
| c |
| a |
| c |
| a |
| b |
| c |
④(3
| a |
| b |
| a |
| b |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、②④ |
在钝角三角形ABC中,a=1,b=2,则最大边c的取值范围是( )
A、(
| ||
B、(
| ||
| C、(2,3) | ||
D、(
|
已知命题p:对任意x∈R,总有x2≥0; q:x=2是方程x+3=0的根,则下列命题为真命题的是( )
| A、¬p∧q | B、p∧¬q |
| C、¬p∧¬q | D、p∧q |
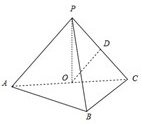 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.