题目内容
已知等差数列{an}中,a1=1,a3=-3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-35,求k的值;
(3)设bn=2n•an,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-35,求k的值;
(3)设bn=2n•an,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用等差数列的通项公式即可得出;
(2)利用等差数列的前n项和公式即可得出;
(3)利用“错位相减法”、等比数列前n项和公式即可得出.
(2)利用等差数列的前n项和公式即可得出;
(3)利用“错位相减法”、等比数列前n项和公式即可得出.
解答:
解:(1)设公差为d,则a3=a1+2d=-3,
∴1+2d=-3,
解得d=-2.
∴an=1-2(n-1)=3-2n.
(2)Sn=
=
=-n2+2n,
∵Sk=-35,
∴-k2+2k=-35,
化为k2-2k-35=0,
解得k=7.
∴k=7.
(3)bn=2n•an=(3-2n)•2n,
∴Tn=1×21-22-3•23-…-(2n-3)•2n,
2Tn=22-23-3×24-…-(2n-5)•2n-(2n-3)•2n+1,
∴-Tn=2-2×22-2×23-…-2•2n+(2n-3)•2n+1
=6-2(2+22+23+…+2n)+(2n-3)•2n+1,
=6-2×
+(2n-3)•2n+1,
∴Tn=-10+2n+2+(3-2n)•2n+1.
∴1+2d=-3,
解得d=-2.
∴an=1-2(n-1)=3-2n.
(2)Sn=
| n(a1+an) |
| 2 |
| n(1+3-2n) |
| 2 |
∵Sk=-35,
∴-k2+2k=-35,
化为k2-2k-35=0,
解得k=7.
∴k=7.
(3)bn=2n•an=(3-2n)•2n,
∴Tn=1×21-22-3•23-…-(2n-3)•2n,
2Tn=22-23-3×24-…-(2n-5)•2n-(2n-3)•2n+1,
∴-Tn=2-2×22-2×23-…-2•2n+(2n-3)•2n+1
=6-2(2+22+23+…+2n)+(2n-3)•2n+1,
=6-2×
| 2(2n-1) |
| 2-1 |
∴Tn=-10+2n+2+(3-2n)•2n+1.
点评:本题考查了“错位相减法”、等差数列与等比数列通项公式及其前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
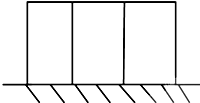 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y(1)请把y表示成x的函数;
(2)当x为何值时,函数取最大值,并求出最大值.
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、“x=-1”是“x2-2x-3=0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x-1<0”的否定是“?x∈R,均有x2+x-1>0” |
| D、命题“已知x,y∈R,若x+y≠5,则x≠1或y≠4”为真命题 |
 某厂生产一种内径为105mm的零件,为了检查该生产流水线的质量情况,随机抽取该流水线上50个零件作为样本测出它们的内径长度(单位:mm),长度的分组区间为[90,95),[95,100),[100,105),[105,110),[110,115),由此得到样本的频率分布直方图,如图所示.已知内径长度在[100,110)之间的零件被认定为一等品,在[95,100)或[110,115)之间的零件被认定为二等品,否则认定为次品.
某厂生产一种内径为105mm的零件,为了检查该生产流水线的质量情况,随机抽取该流水线上50个零件作为样本测出它们的内径长度(单位:mm),长度的分组区间为[90,95),[95,100),[100,105),[105,110),[110,115),由此得到样本的频率分布直方图,如图所示.已知内径长度在[100,110)之间的零件被认定为一等品,在[95,100)或[110,115)之间的零件被认定为二等品,否则认定为次品.