如图，ABCD-A1B1C1D1是棱长为1的正方体．
如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，2AC=AA1=BC=2，D为棱AA1上的点．
已知正三棱柱ABC-A1B1C1的底面边长为8，侧棱长为6，D为AC中点．若点N在直线1上，直线l又在平面α内，则点N，直线l与平面α之间的关系可记作（ ）
| A、N∈l∈α |
| B、N∈l?α |
| C、N?l?α |
| D、N?l∈α |
如图，在直三棱柱ABC-A1B1C1中，AC=BC=AA1，∠ACB=90°，点D是AB的中点．
如图，四边形ABCD为直角梯形，AD∥BC，∠BAD=90°，PA⊥平面ABCD，且PA=AB，M为PC的中点，求证：PB⊥DM．
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，平面PAD⊥平面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为PA的中点．
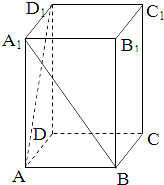在长方体ABCD-A1B1C1D1中，已知DA=DC=4，DD1=3，求异面直线A1B与D1A所成角的余弦值（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在长方体ABCD-A1B1C1D1中，已知DA=DC=4，DD1=3，求异面直线A1B与D1A所成角的余弦值（ ）| A、N∈l∈α |
| B、N∈l?α |
| C、N?l?α |
| D、N?l∈α |
在长方体ABCD-A1B1C1D1中，已知DA=DC=4，DD1=3，求异面直线A1B与D1A所成角的余弦值（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|