题目内容
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,平面PAD⊥平面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为PA的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,平面PAD⊥平面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为PA的中点.(Ⅰ)求证:AD⊥PB;
(Ⅱ)求证:DM∥平面PBC;
(Ⅲ)求四棱锥P-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)取AD中点O,连接OP,OB,OP⊥AD,OB⊥AD,利用线面垂直问题求解.
(Ⅱ)取PB中点N,连接NC,MN,四边形MNCD为平行四边形,根据判定定理证明DM∥平面PBC.
(Ⅲ)根据梯形的性质得出底面ABCD面积为:
×(1+2)×
=
,再利用面面垂直的性质得出四棱锥P-ABCD的高为:OP=1,利用椎体的体积公式即可得到.
(Ⅱ)取PB中点N,连接NC,MN,四边形MNCD为平行四边形,根据判定定理证明DM∥平面PBC.
(Ⅲ)根据梯形的性质得出底面ABCD面积为:
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
解答:
解:(Ⅰ)取AD中点O,连接OP,OB,
∵,AB=AD=2CD=2,△PAD为等腰直角三角形,
∴OP⊥AD,OB⊥AD,
∵OP∩OB=O,
∴AD⊥平面OPB,
∵PB?平面OPB,
∴AD⊥PB;
(Ⅱ)取PB中点N,连接NC,MN,
∵AB=AD=2CD=2,底面ABCD是直角梯形,AB∥CD,M为PA的中点.
∴MN=DC=1,MN∥CD,
∴四边形MNCD为平行四边形,
∴MD∥NC,MD?平面CPB,NC?平面CPB,
∴DM∥平面PBC;
(Ⅲ)∵底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,
∴梯形的高为:2×sin60°=
,
∴底面ABCD面积为:
×(1+2)×
=
,
∵△PAD为等腰直角三角形,∠APD=90,
∴OP=1,OP⊥AD
∵平面PAD⊥平面ABCD,
∴OP⊥平面ABCD,
即四棱锥P-ABCD的高为:OP=1,
∴四棱锥P-ABCD的体积为:
×
×1=

∵,AB=AD=2CD=2,△PAD为等腰直角三角形,
∴OP⊥AD,OB⊥AD,
∵OP∩OB=O,
∴AD⊥平面OPB,
∵PB?平面OPB,
∴AD⊥PB;
(Ⅱ)取PB中点N,连接NC,MN,

∵AB=AD=2CD=2,底面ABCD是直角梯形,AB∥CD,M为PA的中点.
∴MN=DC=1,MN∥CD,
∴四边形MNCD为平行四边形,
∴MD∥NC,MD?平面CPB,NC?平面CPB,
∴DM∥平面PBC;
(Ⅲ)∵底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,
∴梯形的高为:2×sin60°=
| 3 |
∴底面ABCD面积为:
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∵△PAD为等腰直角三角形,∠APD=90,
∴OP=1,OP⊥AD
∵平面PAD⊥平面ABCD,
∴OP⊥平面ABCD,
即四棱锥P-ABCD的高为:OP=1,
∴四棱锥P-ABCD的体积为:
| 1 |
| 3 |
3
| ||
| 2 |
| ||
| 2 |
点评:本题考查了空间几何体的性质,运用直线与平面的平行,垂直的性质,判定定理,解决空间直线平面的位置关系,求解体积,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n都相交 |
| B、与m,n都不相交 |
| C、与m,n中至少一条相交 |
| D、至多与m,n中的一条相交 |
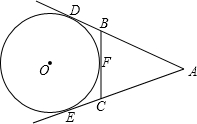 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为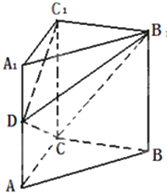 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为棱AA1上的点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为棱AA1上的点.