题目内容
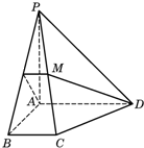 如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.
如图,四边形ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AB,M为PC的中点,求证:PB⊥DM.考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:以A点为坐标原点,以AB,AD,AP方向分别为x,y,z轴正方向建立空间直角坐标系,求出向量
,
的坐标,然后根据两向量数量积为0,两向量垂直,即可得到PB⊥DM;
| PB |
| DM |
解答:
证明:建立如图所示的空间直角坐标系,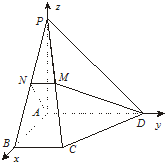 依题意,得
依题意,得
A(0,0,0),B(2,0,0),C(2,1,0),D(0,2,0),
P(0,0,2).(2分)
因为M为PC的中点,所以M(1,
,1).
所以
=(2,0,-2),
=(1,-
,1),
因为
•
=2+0-2=0,
所以PB⊥DM.
 依题意,得
依题意,得A(0,0,0),B(2,0,0),C(2,1,0),D(0,2,0),
P(0,0,2).(2分)
因为M为PC的中点,所以M(1,
| 1 |
| 2 |
所以
| PB |
| DM |
| 3 |
| 2 |
因为
| PB |
| DM |
所以PB⊥DM.
点评:本题考查了直线与平面垂直的性质定理和判定定理的运用,体现了转化思想,考查逻辑思维能力,属于基础题.

练习册系列答案
相关题目
设
=(
,sina),
=(cosa,
)且
∥
,则锐角a为( )
| a |
| 3 |
| 2 |
| b |
| 1 |
| 3 |
| a |
| b |
| A、30° | B、60° |
| C、45° | D、75° |
给出以下命题,不正确的是( )
| A、如果两条平行线中的一条与一个平面相交,那么另一条也和这个平面相交 |
| B、如果直线a和直线b平行,那么直线a平行于经过b的所有的平面 |
| C、如果a和b是异面直线,那么经过a有且只有一个平面与直线b平行 |
| D、空间四边形相邻两边的中点连线,平行于经过另外两条边的平面 |
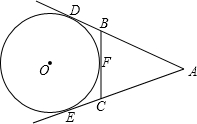 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=18,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=18,则△ABC的周长为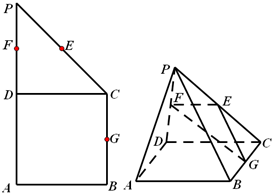 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.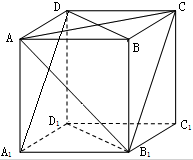 如图,ABCD-A1B1C1D1是棱长为1的正方体.
如图,ABCD-A1B1C1D1是棱长为1的正方体.