题目内容
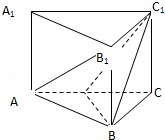 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.
已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.(1)求证:AB1∥平面C1DB;
(2)求异面直线AB1与BC1所成角的余弦值.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)连接B1C交BC1于E,连接DE,利用四边形BCC1B1是平行四边形及其三角形的中位线定理、线面平行的判定定理即可证明;
(2)由(1)知∠DEB或其补角为异面直线AB1与BC1所成的角,再利用余弦定理即可得出.
(2)由(1)知∠DEB或其补角为异面直线AB1与BC1所成的角,再利用余弦定理即可得出.
解答:
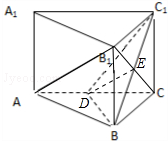 (1)证明:如图所示,
(1)证明:如图所示,
连接B1C交BC1于E,连接DE,
∵四边形BCC1B1是平行四边形,∴B1E=EC.
又AD=DC.
∴DE∥AB1,
而DE?平面C1DB,AB1?平面C1DB,
∴AB1∥平面C1DB.
(2)解:由(1)知∠DEB或其补角为异面直线AB1与BC1所成的角,
在△DEB中,DE=5,BD=4
,BE=5.
∴cos∠DEB=
=
.
 (1)证明:如图所示,
(1)证明:如图所示,连接B1C交BC1于E,连接DE,
∵四边形BCC1B1是平行四边形,∴B1E=EC.
又AD=DC.
∴DE∥AB1,
而DE?平面C1DB,AB1?平面C1DB,
∴AB1∥平面C1DB.
(2)解:由(1)知∠DEB或其补角为异面直线AB1与BC1所成的角,
在△DEB中,DE=5,BD=4
| 3 |
∴cos∠DEB=
| 25+25-48 |
| 2×5×5 |
| 1 |
| 25 |
点评:本题考查了正三棱柱的性质、平行四边形的性质、三角形的中位线定理、线面平行的判定定理、异面直线所成的角、余弦定理等基础知识与基本技能方法,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知A={x|x>2},B={x|x>0},则下列结论正确的是( )
| A、A∈B | B、A⊆B |
| C、A?B | D、A?B |
函数f(x)=1-
在其定义域上是( )
| 2 |
| 2x+1 |
| A、单调递增的奇函数 |
| B、单调递增的减函数 |
| C、偶函数且在(0,+∞)上单调递增 |
| D、偶函数且在(0,+∞)上单调递减 |
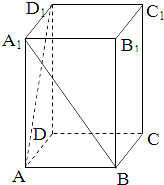 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
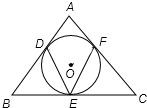
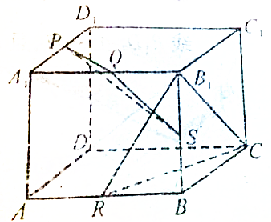 如图,正方体ABCD-A1B1C1D1中,已知Q、P、R、S分别是各棱的中点.求证:平面PQS⊥平面B1RC.
如图,正方体ABCD-A1B1C1D1中,已知Q、P、R、S分别是各棱的中点.求证:平面PQS⊥平面B1RC.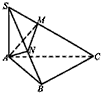 如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.
如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.