题目内容
已知长方体ABCD-A1B1C1D1中，AB=4
，AD=4
，AA1=4，求：
（1）A1B与DC所成的角；
（2）A1C1与AD所成的角；
（3）AC1与DD1所成的余弦值．
| 3 |
| 3 |
（1）A1B与DC所成的角；
（2）A1C1与AD所成的角；
（3）AC1与DD1所成的余弦值．
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：①长方体ABCD-A1B1C1D1中，由A1C1∥AC，知∠BCA是BC和A1C1所成的角，由此能求出BC和A1C1所成的角．
②由AA1⊥平面A1B1C1D1，B1C1?平面A1B1C1D1，能求出AA1和B1C1所成的角．
②由AA1⊥平面A1B1C1D1，B1C1?平面A1B1C1D1，能求出AA1和B1C1所成的角．
解答：
解：如图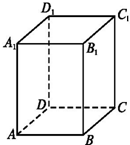
（1）∵DC∥AB，
∴A1B与DC所成的角为∠ABA1；
∵长方体ABCD-A1B1C1D1中，AB=4
，AD=4
，AA1=4，
∴tan∠ABA1=
=
=
，
∴∠ABA1=30°，
∴A1B与DC所成的角为30°；
（2）∵A1C1∥AC，
∴A1C1与AD所成的角是∠DAC，
∵长方体ABCD-A1B1C1D1中，AB=4
，AD=4
，
∴∠DAC=45°，
∴A1C1与AD所成的角是45°．
（2）∵DD1∥CC1，
∴AC1与DD1所成的是∠AC1C，
∵长方体ABCD-A1B1C1D1中，AB=4
，AD=4
，AA1=4，
∴cos∠AC1C=
=
=
=
，
∴AC1与DD1所成的余弦值为
．
（1）∵DC∥AB，∴A1B与DC所成的角为∠ABA1；
∵长方体ABCD-A1B1C1D1中，AB=4
| 3 |
| 3 |
∴tan∠ABA1=
| AA1 |
| AB |
| 4 | ||
4
|
| ||
| 3 |
∴∠ABA1=30°，
∴A1B与DC所成的角为30°；
（2）∵A1C1∥AC，
∴A1C1与AD所成的角是∠DAC，
∵长方体ABCD-A1B1C1D1中，AB=4
| 3 |
| 3 |
∴∠DAC=45°，
∴A1C1与AD所成的角是45°．
（2）∵DD1∥CC1，
∴AC1与DD1所成的是∠AC1C，
∵长方体ABCD-A1B1C1D1中，AB=4
| 3 |
| 3 |
∴cos∠AC1C=
| CC1 |
| AC1 |
| 4 | ||
|
| 4 | ||
4
|
| ||
| 7 |
∴AC1与DD1所成的余弦值为
| ||
| 7 |
点评：本题考查异面直线所成角的大小的求法，根据异面直线所成角的定义关键找出平面角．解题要认真审题，注意等价转化思想的合理运用．
练习册系列答案
相关题目
l是平面α外一条直线，过l作平面β，使α∥β，这样的β（ ）
| A、只能作一个 |
| B、至少可以做一个 |
| C、不存在 |
| D、至多可以作一个 |
若点N在直线1上，直线l又在平面α内，则点N，直线l与平面α之间的关系可记作（ ）
| A、N∈l∈α |
| B、N∈l?α |
| C、N?l?α |
| D、N?l∈α |
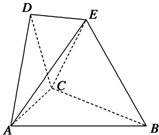在如图所示的空间几何体中，平面ACD⊥平面ABC，△ACD与△ACB是边长为2的等边三角形，BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在∠ABC的平分线上．