题目内容
已知函数f(x)=
,把函数f(x)的图象与直线y=x交点的横坐标按从小到大的顺序排列成一个数列,则该数列的前10项和为 .
|
考点:数列与函数的综合
专题:计算题,数形结合,函数的性质及应用,等差数列与等比数列
分析:根据函数的零点的定义,构造两函数图象的交点,交点的横坐标即为函数的零点,再通过数列及通项公式的概念和求和公式即可得所求的解.
解答:
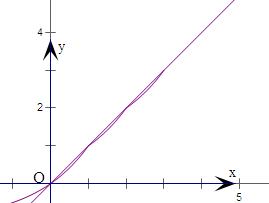 解:当x∈(-∞,1]时,由g(x)=f(x)-x=2x-1-x=0,
解:当x∈(-∞,1]时,由g(x)=f(x)-x=2x-1-x=0,
得2x=x+1.令y=2x,y=x+1.
在同一个坐标系内作出两函数在区间(-∞,1]上的图象,
由图象易知交点为(0,0)和(1,1),
故得到函数的零点为x1=0,x2=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1
=2x-1-1+1=2x-1,
由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.令y=2x-1,y=x.
在同一个坐标系内作出两函数在区间(1,2]上的图象,
由图象易知交点为(2,2),故得到函数的零点为x3=2.
当x∈(2,3]时,x-1∈(1,2],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,
由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2+1,y=x.
在同一个坐标系内作出两函数在区间(2,3]上的图象,
由图象易知交点为(3,3),故得到函数的零点为x4=3.
依此类推,当x∈(3,4],x∈(4,5],…,x∈(n,n+1]时,
构造的两函数图象的交点依次为(4,4),(5,5),…,(n+1,n+1),
得对应的零点分别为x=4,x=5,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.
其对应的数列的通项公式为an=n-1.
则该数列前10项和为
=45.
故答案为:45.
 解:当x∈(-∞,1]时,由g(x)=f(x)-x=2x-1-x=0,
解:当x∈(-∞,1]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.
在同一个坐标系内作出两函数在区间(-∞,1]上的图象,
由图象易知交点为(0,0)和(1,1),
故得到函数的零点为x1=0,x2=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1
=2x-1-1+1=2x-1,
由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.令y=2x-1,y=x.
在同一个坐标系内作出两函数在区间(1,2]上的图象,
由图象易知交点为(2,2),故得到函数的零点为x3=2.
当x∈(2,3]时,x-1∈(1,2],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,
由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2+1,y=x.
在同一个坐标系内作出两函数在区间(2,3]上的图象,
由图象易知交点为(3,3),故得到函数的零点为x4=3.
依此类推,当x∈(3,4],x∈(4,5],…,x∈(n,n+1]时,
构造的两函数图象的交点依次为(4,4),(5,5),…,(n+1,n+1),
得对应的零点分别为x=4,x=5,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.
其对应的数列的通项公式为an=n-1.
则该数列前10项和为
| 9×10 |
| 2 |
故答案为:45.
点评:本题主要考查了函数零点的概念及零点的求法、数列的概念及简单表示;培养学生观察、分析、归纳、推理的能力;解题中使用了数形结合和分类讨论的数学方法和数学思想.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知集合A={x|x=sin
,k∈Z},B={x||x-1|≤1},则A∩B=( )
| kπ |
| 2 |
| A、{-1,0} | B、{1,0} |
| C、{0} | D、{1} |
在△ABC中,|
|=2,|
|=1,已知D是BC边上一点,AD平分∠BAC,
=λ
+μ
则( )
| AB |
| AC |
| AD |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
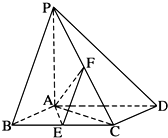 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
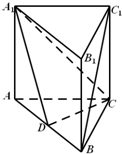 如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.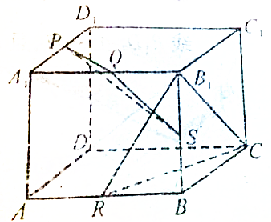 如图,正方体ABCD-A1B1C1D1中,已知Q、P、R、S分别是各棱的中点.求证:平面PQS⊥平面B1RC.
如图,正方体ABCD-A1B1C1D1中,已知Q、P、R、S分别是各棱的中点.求证:平面PQS⊥平面B1RC.