题目内容
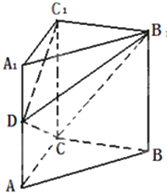 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为棱AA1上的点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为棱AA1上的点.(1)若D为AA1的中点,求证:平面B1CD⊥平面B1C1D;
(2)若直线B1D与平面ACC1A1所成角为45°,求AD的长.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)D为AA1中点,推出平面B1CD内的直线CD,垂直平面B1C1D内的两条相交直线DC1,B1C1可得CD⊥平面B1C1D,即可得到平面B1CD⊥平面B1C1D;
(2)证明B1C1⊥平面ACC1A1,可得∠B1DC1是直线B1D与平面ACC1A1所成角,进而求出C1D=2,A1D=
,即可求AD的长.
(2)证明B1C1⊥平面ACC1A1,可得∠B1DC1是直线B1D与平面ACC1A1所成角,进而求出C1D=2,A1D=
| 3 |
解答:
(1)证明:∵∠A1C1B1=∠ACB=90°
∴B1C1⊥A1C1
又由直三棱柱性质知B1C1⊥CC1,
∴B1C1⊥平面ACC1A1.
∴B1C1⊥CD.
由AA1=BC=2AC=2,D为AA1中点,可知DC=DC1=
,
∴DC2+DC12=CC12=4即CD⊥DC1,
又B1C1⊥CD,∴CD⊥平面B1C1D
又CD?平面B1CD
故平面B1CD⊥平面B1C1D;
(2)解:∵直三棱柱ABC-A1B1C1中,∠ACB=90°,
∴B1C1⊥平面ACC1A1,
∴∠B1DC1是直线B1D与平面ACC1A1所成角,
∵直线B1D与平面ACC1A1所成角为45°,BC=2,
∴C1D=2,
∵A1C1=1,
∴A1D=
,
∵AA1=2,
∴AD=2-
.
∴B1C1⊥A1C1
又由直三棱柱性质知B1C1⊥CC1,
∴B1C1⊥平面ACC1A1.
∴B1C1⊥CD.
由AA1=BC=2AC=2,D为AA1中点,可知DC=DC1=
| 2 |
∴DC2+DC12=CC12=4即CD⊥DC1,
又B1C1⊥CD,∴CD⊥平面B1C1D
又CD?平面B1CD
故平面B1CD⊥平面B1C1D;
(2)解:∵直三棱柱ABC-A1B1C1中,∠ACB=90°,
∴B1C1⊥平面ACC1A1,
∴∠B1DC1是直线B1D与平面ACC1A1所成角,
∵直线B1D与平面ACC1A1所成角为45°,BC=2,
∴C1D=2,
∵A1C1=1,
∴A1D=
| 3 |
∵AA1=2,
∴AD=2-
| 3 |
点评:本题考查平面与平面垂直的判定,考查线面角,考查学生空间想象能力,逻辑思维能力、计算能力,是中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知集合A={x|
<0},B={
|4<x<12,1<y<2},则A∪B=( )
| ln(2x-1) |
| x-5 |
| x |
| y |
| A、(1,12) |
| B、(1,6) |
| C、(2,5) |
| D、(4,5) |
l是平面α外一条直线,过l作平面β,使α∥β,这样的β( )
| A、只能作一个 |
| B、至少可以做一个 |
| C、不存在 |
| D、至多可以作一个 |
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,平面PAD⊥平面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为PA的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,平面PAD⊥平面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为PA的中点.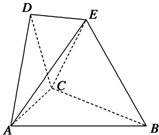 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.