题目内容
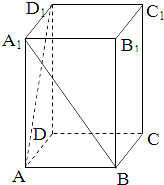 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:利用长方体的性质首先找到异面直线A1B与D1A所成角为∠A1BC1,然后利用勾股定理求此角所在的三角形各边,最后利用余弦定理求内角大小.
解答:
解:因为AD1∥BC1,
所以异面直线A1B与D1A所成角为∠A1BC1,
因为长方体ABCD-A1B1C1D1中,DA=DC=4,DD1=3,
所以A1B=5,BC1=5,A1C1=4
,
所以cos∠A1BC1,=
=
=
;
故选B.
所以异面直线A1B与D1A所成角为∠A1BC1,
因为长方体ABCD-A1B1C1D1中,DA=DC=4,DD1=3,
所以A1B=5,BC1=5,A1C1=4
| 2 |
所以cos∠A1BC1,=
| A1B2+BC12-A1C12 |
| 2A1B×BC1 |
52+52-(4
| ||
| 2×5×5 |
| 9 |
| 25 |
故选B.
点评:本题考查了异面直线所成的角的求法以及利用余弦定理求角的问题;关键是找到异面直线所成的角,然后求之属于经常考查的题型.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
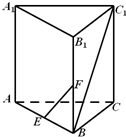 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、135° |
| C、60° | D、120° |
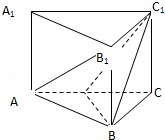 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.
已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.