对于非空数集A,若实数M满足对任意的a∈A恒有a≤M,则M为A的上界;若A的所有上界中存在最小值,则称此最小值为A的上确界,那么下列函数的值域中具有上确界的是( )
A、y=
| ||||
B、y=(-
| ||||
C、y=
| ||||
| D、y=lnx |
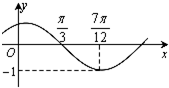 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
A、y=
| ||||
B、y=(-
| ||||
C、y=
| ||||
| D、y=lnx |
 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|