题目内容
设函数f(x)=Acos(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间[
,
]上具有单调性,且f(
)=f(
)=-f(
),则f(x)的最小正周期为 .
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 4 |
考点:三角函数的周期性及其求法,余弦函数的图象
专题:三角函数的图像与性质
分析:由题意可得可得函数f(x)的一条对称轴方程为x=
=
,x=
离最近对称轴距离为
-
=
,
离最近对称轴的距离也为
,可得
=2×
+(
-
),由此求得周期T的值.
| ||||
| 2 |
| 7π |
| 12 |
| π |
| 2 |
| 7π |
| 12 |
| π |
| 2 |
| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| T |
| 2 |
| π |
| 12 |
| π |
| 2 |
| π |
| 4 |
解答:
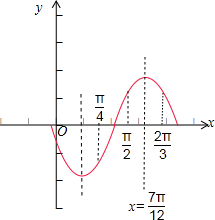 解:由f(
解:由f(
)=f(
),可得函数f(x)的一条对称轴
方程为x=
=
,
则x=
离最近对称轴距离为
-
=
,
又f(
)=-f(
),且f(x)在区间[
,
]上具有单调性,
故
离最近对称轴的距离也为
,
∴
=2×
+(
-
)=
,∴T=
,
故答案为:
.
 解:由f(
解:由f(| π |
| 2 |
| 2π |
| 3 |
方程为x=
| ||||
| 2 |
| 7π |
| 12 |
则x=
| π |
| 2 |
| 7π |
| 12 |
| π |
| 2 |
| π |
| 12 |
又f(
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故
| π |
| 4 |
| π |
| 12 |
∴
| T |
| 2 |
| π |
| 12 |
| π |
| 2 |
| π |
| 4 |
| 5π |
| 12 |
| 5π |
| 6 |
故答案为:
| 5π |
| 6 |
点评:本题考查f(x)=Asin(ωx+φ)型图象的形状,考查了学生灵活处理问题和解决问题的能力,是中档题.

练习册系列答案
相关题目