题目内容
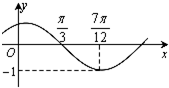函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值,三角函数的图像与性质
分析：首先根据函数的图象现确定函数解析式，进一步利用平移变换求出结果．
解答：
解：根据函数的图象：A=1
又
=
-
解得：T=π
则：ω=2
当x=
时，f（
）=sin（
+φ）=0
解得：φ=
所以：f（x）=sin（2x+
）
要得到g（x）=sin2x的图象只需将函数图象向右平移
个单位即可．
故选：A
又
| T |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
解得：T=π
则：ω=2
当x=
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解得：φ=
| π |
| 3 |
所以：f（x）=sin（2x+
| π |
| 3 |
要得到g（x）=sin2x的图象只需将函数图象向右平移
| π |
| 6 |
故选：A
点评：本题考查的知识要点：函数图象的平移变换，函数解析式的求法．属于基础题型
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=
x3+
x2+（a+b）x+c（a，b，c∈R）的两个极值点分别为x1，x2，且x1∈（0，1），x2∈（1，+∞），z=2a-b，则z的取值范围是（ ）
| 1 |
| 3 |
| a |
| 2 |
| A、（-∞，3] |
| B、（-∞，-3） |
| C、[-3，+∞） |
| D、（-3，+∞） |
设集合A={2，4，6，8，10}，B={1，9，25，49，81，100}，下面的对应关系能构成从A到B的映射的是（ ）
| A、f：x→（2x-1）2 |
| B、f：x→（2x-3）2 |
| C、f：x→x2-2x-1 |
| D、f：x→（x-1）2 |
中心在原点，焦点在x轴上的双曲线的一条渐近线与直线y=
x+1平行，则它的离心率为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
过抛物线x2=y焦点的直线l交抛物线于A、B两点，且|AB|=4，则线段AB中点到x轴的距离是（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |