已知
=（-1，2），
=（2，λ），且
与
的夹角为钝角，则实数λ的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、（-∞，1） |
| B、（0，1） |
| C、（1，∞） |
| D、（-∞，-4）∪（-4，1） |
向量平移是简化函数解析式、研究函数性质的重要方法，已知函数y=f（x）的图象按
=（a，b）平移得y-b=f（x-a）的图象，函数y=x2-4x+
+1的图象按
=（-2，3）平移得到函数y=f（x）的图象，若方程f（x）=a有2个不相等的实数根，则实数a的取值集合为（ ）
| m |
| 2 |
| x-2 |
| n |
| A、{-3} |
| B、{3} |
| C、{a|a＞-3|} |
| D、{a|a＞3} |
已知向量
=(cos2α，
)，
=(
，sin2α)，且-
≤α≤
，则“α=
”是“
⊥
”的（ ）
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 12 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
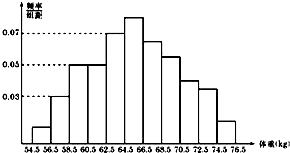为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁～18岁的男生体重（kg），得到频率分布直方图如图：根据如图可得这100名学生中体重在[60.5，64.5]的学生人数是