题目内容
数列{an}的前n项和Sn=
n2-2n(n∈N*),数列{bn}满足bn=
,
(1)求数列{an}的通项公式;
(2)计算了b1,b2,b3,并猜想数列{bn}中的最大项和最小项(不需要证明)
| 1 |
| 2 |
| an+1 |
| an |
(1)求数列{an}的通项公式;
(2)计算了b1,b2,b3,并猜想数列{bn}中的最大项和最小项(不需要证明)
考点:数列递推式
专题:等差数列与等比数列
分析:(1)利用公式an=
求解.
(2)bn=
=
=1+
=1+
,由此能求出b1,b2,b3,并猜想数列{bn}中的最大项和最小项.
|
(2)bn=
| an+1 |
| an |
n-
| ||
n-
|
| 1 | ||
n-
|
| 2 |
| 2n-5 |
解答:
解:(1)∵数列{an}的前n项和Sn=
n2-2n(n∈N*),
∴a1=S1=
-2=-
,
当n≥2时,an=Sn-Sn-1=(
n2-2n)-[
(n-1)2-2(n-1)]=n-
,
n=1时,上式成立,
∴an=n-
.
(2)bn=
=
=1+
=1+
,
b1=1+
=
,
b2=1+
=-1,
b3=1+
=3.
由题意得数列{bn}中的最大项为b3=3,最小项为b2=-1.
| 1 |
| 2 |
∴a1=S1=
| 1 |
| 2 |
| 3 |
| 2 |
当n≥2时,an=Sn-Sn-1=(
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
n=1时,上式成立,
∴an=n-
| 5 |
| 2 |
(2)bn=
| an+1 |
| an |
n-
| ||
n-
|
| 1 | ||
n-
|
| 2 |
| 2n-5 |
b1=1+
| 2 |
| 2-5 |
| 1 |
| 3 |
b2=1+
| 2 |
| 4-5 |
b3=1+
| 2 |
| 6-5 |
由题意得数列{bn}中的最大项为b3=3,最小项为b2=-1.
点评:本题考查数列的通项公式的求法,考查数列中最大项和最小项的合理猜想,解题时要注意公式an=
的合理运用.
|

练习册系列答案
相关题目
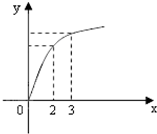 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A、f′(2)<f′(3)<f(3)-f(2) |
| B、f′(3)<f(3)-f(2)<f′(2) |
| C、f′(3)<f′(2)<f(3)-f(2) |
| D、f(3)-f(2)<f′(2)<f′(3) |
已知等差数列{an}共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )
| A、d=1 | ||
B、d=
| ||
| C、a6=5 | ||
| D、a6=-5 |
已知向量
=(cos2α,
),
=(
,sin2α),且-
≤α≤
,则“α=
”是“
⊥
”的( )
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 12 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知一个程序框图如图所示,若输入n=6,则该程序运行的结果是( )


| A、2 | B、3 | C、4 | D、15 |