题目内容
已知向量
=(cos2α,
),
=(
,sin2α),且-
≤α≤
,则“α=
”是“
⊥
”的( )
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 12 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分必要条件的定义,结合向量的运算性质,分别证明充分性和必要性,从而得到答案.
解答:
解:若α=
,则
=(cos
,
),
=(
,sin
),
∴
•
=-
×
+
×
=0,
∴
⊥
,是充分条件;
若
⊥
,则
•
=
cos2α+
sin2α=sin(
+2α)=0,
由-
≤α≤
,得到
+2α=0或
+2α=π,
解得:α=-
或α=
,不是必要条件,
故选:A.
| 5π |
| 12 |
| a |
| 5π |
| 6 |
| ||
| 2 |
| b |
| 1 |
| 2 |
| 5π |
| 6 |
∴
| a |
| b |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴
| a |
| b |
若
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
解得:α=-
| π |
| 12 |
| 5π |
| 12 |
故选:A.
点评:本题考查了充分必要条件,考查了向量的运算性质,是一道基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
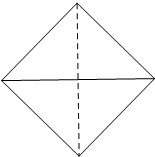 已知四面体S-ABC的所有棱长都相等,它的俯视图如图所示,是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图如图所示,是一个边长为| 2 |
| A、6π | B、4π | C、8π | D、3π |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<