题目内容
向量平移是简化函数解析式、研究函数性质的重要方法,已知函数y=f(x)的图象按
=(a,b)平移得y-b=f(x-a)的图象,函数y=x2-4x+
+1的图象按
=(-2,3)平移得到函数y=f(x)的图象,若方程f(x)=a有2个不相等的实数根,则实数a的取值集合为( )
| m |
| 2 |
| x-2 |
| n |
| A、{-3} |
| B、{3} |
| C、{a|a>-3|} |
| D、{a|a>3} |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:根据函数图象平移规律得出f(x)=x2+
,结合导数,图象解决a的取值问题,与函数图象的交点个数问题.
| 2 |
| x |
解答:
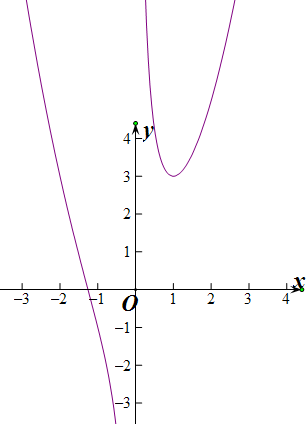 解:根据函数图象平移规律得出:
解:根据函数图象平移规律得出:
函数y=x2-4x+
+1的图象按
=(-2,3)平移得到函数y=f(x)的图象,
∴f(x)=(x+2)2-4(x+2)+
+1+3=x2+
,
∵f(x)=x2+
,
g(x)=a,
f′(x)=2x-
=
,
f′(x)=0,x=1,
x>1时,f′(x)>0,
x<0,或0<x<1时,f′(x)<0,
∴f(x)在(1,+∞)单调递增,(-∞,0)(0,1)单调递减,
f(x)极小值=f(1)=3,
根据图象可得出:g(x)=3,与f(x)有2个交点,
故a=3,方程f(x)=a有2个不相等的实数根,
故选:B
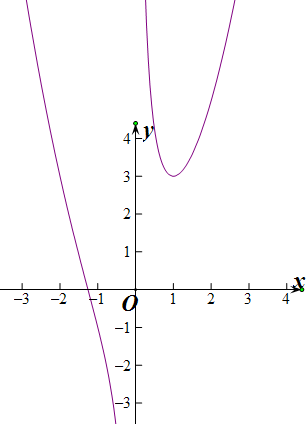 解:根据函数图象平移规律得出:
解:根据函数图象平移规律得出:函数y=x2-4x+
| 2 |
| x-2 |
| n |
∴f(x)=(x+2)2-4(x+2)+
| 2 |
| x |
| 2 |
| x |
∵f(x)=x2+
| 2 |
| x |
g(x)=a,
f′(x)=2x-
| 2 |
| x2 |
| 2(x3-1) |
| x2 |
f′(x)=0,x=1,
x>1时,f′(x)>0,
x<0,或0<x<1时,f′(x)<0,
∴f(x)在(1,+∞)单调递增,(-∞,0)(0,1)单调递减,
f(x)极小值=f(1)=3,
根据图象可得出:g(x)=3,与f(x)有2个交点,
故a=3,方程f(x)=a有2个不相等的实数根,
故选:B
点评:本题考查了函数的性质,运用导数判断单调性,极值,结合函数的图象判断交点个数,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
巳知角α的终边与单位圆交于点(-
,
),则sin2α的值为( )
2
| ||
| 5 |
| ||
| 5 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
由如图的流程图输出的s为( )


| A、64 | B、512 |
| C、128 | D、256 |
已知
=(-1,2),
=(2,λ),且
与
的夹角为钝角,则实数λ的取值范围是( )
| a |
| b |
| a |
| b |
| A、(-∞,1) |
| B、(0,1) |
| C、(1,∞) |
| D、(-∞,-4)∪(-4,1) |
