题目内容
已知各项均为正数的数列{an}的前n项和为Sn满足4Sn=a
+2an.
(1)求a1的值;
(2)求{an}的通项公式;
(3)求证:
+
+…+
<2,n∈NΦ.
2 n |
(1)求a1的值;
(2)求{an}的通项公式;
(3)求证:
| 4 | ||
|
| 4 | ||
|
| 4 | ||
|
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)4Sn=a
+2an.令n=1,可得4a1=
+2a1,解出即可.
(2)当n≥2时,4an=4Sn-4Sn-1,化为(an+an-1)(an-an-1-2)=0,可得an-an-1=2,利用等差数列的通项公式即可得出.
(3)当n=1时,
=1<2成立.当n≥2时,
<
=
-
.利用“裂项求和”即可得出.
2 n |
| a | 2 1 |
(2)当n≥2时,4an=4Sn-4Sn-1,化为(an+an-1)(an-an-1-2)=0,可得an-an-1=2,利用等差数列的通项公式即可得出.
(3)当n=1时,
| 4 | ||
|
| 1 |
| n2 |
| 1 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
解答:
(1)解:∵4Sn=a
+2an.令n=1,可得4a1=
+2a1,a1>0,解得a1=2.
(2)解:当n≥2时,4an=4Sn-4Sn-1=
+2an-(
+2an-1),
化为(an+an-1)(an-an-1-2)=0,
∵an>0,an-1>0,
∴an-an-1=2,
∴数列{an}是等差数列,
∴an=2+2(n-1)=2n.
(3)证明:当n=1时,
=1<2成立.
当n≥2时,
<
=
-
.
∴
+
+…+
=
+
+
+…+
<1+(1-
)+(
-
)+…+(
-
)=2-
<2.
2 n |
| a | 2 1 |
(2)解:当n≥2时,4an=4Sn-4Sn-1=
| a | 2 n |
| a | 2 n-1 |
化为(an+an-1)(an-an-1-2)=0,
∵an>0,an-1>0,
∴an-an-1=2,
∴数列{an}是等差数列,
∴an=2+2(n-1)=2n.
(3)证明:当n=1时,
| 4 | ||
|
当n≥2时,
| 1 |
| n2 |
| 1 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
∴
| 4 | ||
|
| 4 | ||
|
| 4 | ||
|
| 1 |
| 1 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
点评:本题考查了递推式的应用、等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=sinx+
cosx的图象关于直线x=a对称,则最小正实数a的值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在直角三角形ABC中,∠C=
,AC=3,取点D使
=2
,那么
•
=( )
| π |
| 2 |
| BD |
| DA |
| CD |
| CA |
| A、3 | B、4 | C、5 | D、6 |
下列等式成立的是( )
| A、2cosx=3 | ||
| B、2sinx=3 | ||
C、sin2x=
| ||
| D、sinx+cosx=2 |
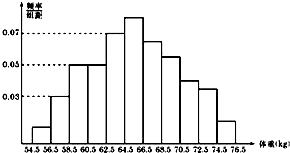 为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这100名学生中体重在[60.5,64.5]的学生人数是
为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这100名学生中体重在[60.5,64.5]的学生人数是 如图,在直三棱柱ABC-A1B1C1中,AB=AC=
如图,在直三棱柱ABC-A1B1C1中,AB=AC=