设函数f（x）（x∈R）的导函数为f′（x），满足f′（x）＞f（x），则当a＞0时，f（a）与eaf（0）的大小关系为（　　）
A、f（a）＞eaf（0）
B、f（a）＜eaf（0）
C、f（a）=eaf（0）
D、不能确定
已知函数f（x）=
1
3
x3-
1
2
x2+x，则f′（1）的值为（　　）
A、0B、1C、2D、3
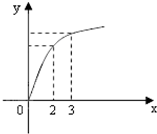已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（　　）
A、f′（2）＜f′（3）＜f（3）-f（2）
B、f′（3）＜f（3）-f（2）＜f′（2）
C、f′（3）＜f′（2）＜f（3）-f（2）
D、f（3）-f（2）＜f′（2）＜f′（3）
一束光线从点A（-1，1）出发经x轴反射，到达圆C：（x-2）2+（y-2）2=1上一点的最短路程是
 
．
已知数列{an}是一个公差大于零的等差数列，且a3a6=55，a2+a7=16，数列{bn}的前n项和为Sn，且Sn=2bn-2．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=
an
bn
，Tn=c1+c2+…+cn，试比较Tn与
4n
2n+1
的大小，并予以证明．
已知双曲线
x2
a2
-
y2
b2
=1的两个焦点分别为F1、F2，该双曲线与抛物线y2=8x有一个公共的焦点F1，且两曲线的一个交点为P，|F1P|=5，则∠F1PF2的大小为
 
．（结果用反三角函数表示）
定义在R上的函数f（x）满足f（x+4）-f（x）=0，且已知x∈（0，4]时，f（x）=
sin
π
2
x，x∈(0，2]
1-|x-3|，x∈(2，4]
，则函数g（x）=5f（x）-x零点个数为（　　）
A、3B、4C、5D、6
已知sin（α+
π
4
）=
1
2
，α∈（0，π），则cosα=
 
．
把一颗骰子投掷两次，第一次出现的点数记为a，第二次出现的点数记为b．已知直线l1：x+2y=2，直线l2：ax+by=4，试求：
（Ⅰ）直线l1、l2相交的概率；   
（Ⅱ）直线l1、l2平行的概率．
设曲线y=ax3在点（1，a）处的切线与直线6x-y+2=0平行，则a=（　　）
A、2
B、-2
C、
1
2
D、-
1
2
 0  202891  202899  202905  202909  202915  202917  202921  202927  202929  202935  202941  202945  202947  202951  202957  202959  202965  202969  202971  202975  202977  202981  202983  202985  202986  202987  202989  202990  202991  202993  202995  202999  203001  203005  203007  203011  203017  203019  203025  203029  203031  203035  203041  203047  203049  203055  203059  203061  203067  203071  203077  203085  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网