题目内容
已知sin(α+
)=
,α∈(0,π),则cosα= .
| π |
| 4 |
| 1 |
| 2 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:依题意,可求得α=
-
,再利用特殊角的三角函数值与两角差的余弦计算即可.
| 5π |
| 6 |
| π |
| 4 |
解答:
解:∵α∈(0,π),
∴(α+
)∈(
,
);
又sin(α+
)=
,
∴α+
=
,
∴cosα=cos(
-
)=cos
cos
+sin
sin
=-
×
+
×
=
.
故答案为:
.
∴(α+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
又sin(α+
| π |
| 4 |
| 1 |
| 2 |
∴α+
| π |
| 4 |
| 5π |
| 6 |
∴cosα=cos(
| 5π |
| 6 |
| π |
| 4 |
| 5π |
| 6 |
| π |
| 4 |
| 5π |
| 6 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
故答案为:
| ||||
| 4 |
点评:本题考查两角差的余弦与正弦,求得α=
-
是关键,考查运算求解能力,属于中档题.
| 5π |
| 6 |
| π |
| 4 |

练习册系列答案
相关题目
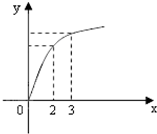 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A、f′(2)<f′(3)<f(3)-f(2) |
| B、f′(3)<f(3)-f(2)<f′(2) |
| C、f′(3)<f′(2)<f(3)-f(2) |
| D、f(3)-f(2)<f′(2)<f′(3) |
已知向量
=(cos2α,
),
=(
,sin2α),且-
≤α≤
,则“α=
”是“
⊥
”的( )
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 12 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
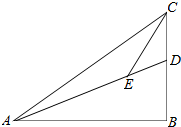 如图,△ABC中,∠ABC=90°,点D在BC边上,点E在AD上.
如图,△ABC中,∠ABC=90°,点D在BC边上,点E在AD上.