题目内容
已知双曲线
-
=1的两个焦点分别为F1、F2,该双曲线与抛物线y2=8x有一个公共的焦点F1,且两曲线的一个交点为P,|F1P|=5,则∠F1PF2的大小为 .(结果用反三角函数表示)
| x2 |
| a2 |
| y2 |
| b2 |
考点:抛物线的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意双曲线与抛物线y2=8x有一个公共的焦点F,可求得双曲线的两个焦点的坐标,再由两曲线的一个交点为P,|PF|=5,利用抛物线的性质可以求得P点的坐标,再由两点间距离公式可以求得P点到另一个焦点的距离,由此即可利用余弦定理求出∠FPF'的余弦值,用反三角函数表示出角即可.
解答:
解:由题意知抛物线的焦点是(2,0),故双曲线的焦点是(2,0)与(-2,0)
又两曲线的一个交点为P,|PF|=5,由抛物线的性质可求得P的横坐标为3,代入抛物线方程可求得P点的纵坐标是±2
不妨令P(3,2
),由两点间距离公式求得,P到另一个焦点的距离是7
在△FPF'中,由余弦定理得cos∠FPF'=
=
,
∴∠FPF'的大小为arccos
,
故答案为:arccos
.
又两曲线的一个交点为P,|PF|=5,由抛物线的性质可求得P的横坐标为3,代入抛物线方程可求得P点的纵坐标是±2
| 6 |
不妨令P(3,2
| 6 |
在△FPF'中,由余弦定理得cos∠FPF'=
| 72+52-42 |
| 2×7×5 |
| 29 |
| 35 |
∴∠FPF'的大小为arccos
| 29 |
| 35 |
故答案为:arccos
| 29 |
| 35 |
点评:本题考查圆锥曲线的综合,求解本题的关键是根据抛物线的性质求出双曲线的两个焦点的坐标以及两曲线交点的坐标,由此求出点P到两个焦点的距离,在这个焦点三角形中利用余弦定理求出∠FPF'的余弦值,再用反三角函数表示,本题的解题思路要注意从图形上推理,圆锥曲线的题解题时要注意图形的作用,数形结合是解析几何的根本.

练习册系列答案
相关题目
若(2+2i)(1-mi)(i为虚数单位)为纯虚数,则实数m的值等于( )
| A、1 | B、-1 | C、0 | D、1或-1 |
设函数f(x)(x∈R)的导函数为f′(x),满足f′(x)>f(x),则当a>0时,f(a)与eaf(0)的大小关系为( )
| A、f(a)>eaf(0) |
| B、f(a)<eaf(0) |
| C、f(a)=eaf(0) |
| D、不能确定 |
图中的小网格由等大的小正方形拼成,则向量
-
=( )

| a |
| b |

| A、e1+3e2 |
| B、-e1-3e2 |
| C、-e1+3e2 |
| D、e1-3e2 |
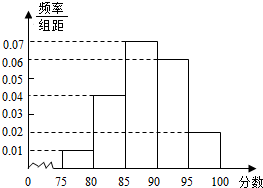 某工厂招聘工人,在一次大型的招聘中,其中1000人的笔试成绩的频率分布直方图如图所示,按厂方规定85分以上(含85分)可以直接录用.
某工厂招聘工人,在一次大型的招聘中,其中1000人的笔试成绩的频率分布直方图如图所示,按厂方规定85分以上(含85分)可以直接录用.