题目内容
已知数列{an}是一个公差大于零的等差数列,且a3a6=55,a2+a7=16,数列{bn}的前n项和为Sn,且Sn=2bn-2.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=
,Tn=c1+c2+…+cn,试比较Tn与
的大小,并予以证明.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=
| an |
| bn |
| 4n |
| 2n+1 |
考点:数列与不等式的综合,等差数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)设等差数列{an}的公差为d(d>0),由已知列方程组求解首项和公差,得到数列{an}的通项公式,再由Sn=2bn-2确定数列{bn}为等比数列,由等比数列的通项公式得答案;
(Ⅱ)把数列{an},{bn}的通项公式代入cn=
,由错位相减法求其前n项和,然后利用归纳猜想得到当n=1,2时,Tn<
;当n≥3时,Tn>
.最后利用数学归纳法证明.
(Ⅱ)把数列{an},{bn}的通项公式代入cn=
| an |
| bn |
| 4n |
| 2n+1 |
| 4n |
| 2n+1 |
解答:
解:(Ⅰ)依题意,设等差数列{an}的公差为d(d>0),
则
,把②代入①得:(16-3d)(16+3d)=220,
解得:d2=4,
∵d>0,∴d=2,a1=1,
∴an=2n-1.
当n=1时,S1=2b1-2,b1=2,
当n≥2时,bn=Sn-Sn-1=(2bn-2)-(2bn-1-2)=2bn-2bn-1,
∴bn=2bn-1,
∴{bn}是以2为首项,以2为公比的等比数列,则bn=2n;
(Ⅱ)cn=
=
,
Tn=
+
+…+
,
Tn=
+
+…+
+
,
两式作差得:
Tn=
+
+
+…+
-
=
+
-
=
-
,
∴Tn=3-
.
Tn-
=3-
-
=
.
要比较Tn与
的大小,只需比较2n与2n+1的大小即可.
由2<2×1+1,222×3+1,24>2×4+1,
可猜想当n≥3时,2n>2n+1.
下面用数学归纳法证明:
当n=3时显然成立;假设当n=k(k≥3)时猜想成立,即2k>2k+1,
当n=k+1时,2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1.
∴当n=k+1时猜想成立.
综上,当n=1,2时,Tn<
;当n≥3时,Tn>
.
则
|
解得:d2=4,
∵d>0,∴d=2,a1=1,
∴an=2n-1.
当n=1时,S1=2b1-2,b1=2,
当n≥2时,bn=Sn-Sn-1=(2bn-2)-(2bn-1-2)=2bn-2bn-1,
∴bn=2bn-1,
∴{bn}是以2为首项,以2为公比的等比数列,则bn=2n;
(Ⅱ)cn=
| an |
| bn |
| 2n-1 |
| 2n |
Tn=
| 1 |
| 2 |
| 3 |
| 22 |
| 2n-1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 23 |
| 2n-3 |
| 2n |
| 2n-1 |
| 2n+1 |
两式作差得:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| 2 |
| 23 |
| 2 |
| 2n |
| 2n-1 |
| 2n+1 |
=
| 1 |
| 2 |
| ||||
1-
|
| 2n-1 |
| 2n+1 |
| 3 |
| 2 |
| 2n+3 |
| 2n+1 |
∴Tn=3-
| 2n+3 |
| 2n |
Tn-
| 4n |
| 2n+1 |
| 2n+3 |
| 2n |
| 4n |
| 2n+1 |
| (2n+3)(2n-2n-1) |
| (2n+1)2n |
要比较Tn与
| 4n |
| 2n+1 |
由2<2×1+1,222×3+1,24>2×4+1,
可猜想当n≥3时,2n>2n+1.
下面用数学归纳法证明:
当n=3时显然成立;假设当n=k(k≥3)时猜想成立,即2k>2k+1,
当n=k+1时,2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1.
∴当n=k+1时猜想成立.
综上,当n=1,2时,Tn<
| 4n |
| 2n+1 |
| 4n |
| 2n+1 |
点评:本题考查了等差数列的性质,考查了错位相减法求数列的前n项和,训练了数学归纳法证明数列不等式,是难题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
设曲线y=ax3在点(1,a)处的切线与直线6x-y+2=0平行,则a=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
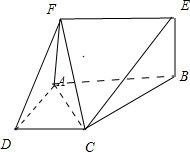 已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4
已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4 某高校招收了100名体育运动员,按身高分组,得到的频率分布表如下左图所示.
某高校招收了100名体育运动员,按身高分组,得到的频率分布表如下左图所示.