题目内容
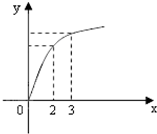已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）| A、f′（2）＜f′（3）＜f（3）-f（2） |
| B、f′（3）＜f（3）-f（2）＜f′（2） |
| C、f′（3）＜f′（2）＜f（3）-f（2） |
| D、f（3）-f（2）＜f′（2）＜f′（3） |
考点：导数的运算
专题：导数的概念及应用
分析：由题意，作出f′（3）、f（3）-f（2）、f′（2）所表示的几何意义，从而求解．
解答：
解：如下图：
f′（3）、f（3）-f（2）、f′（2）分别表示了直线n，m，l的斜率，
故0＜f′（3）＜f（3）-f（2）＜f′（2），
故选B．
f′（3）、f（3）-f（2）、f′（2）分别表示了直线n，m，l的斜率，
故0＜f′（3）＜f（3）-f（2）＜f′（2），
故选B．
点评：本题考查了学生的作图能力及对导数的几何意义的理解，属于中档题．
练习册系列答案
相关题目
若原点O到直线ax+by+c=0的距离为1，则有（ ）
| A、c=1 | ||
B、c=
| ||
| C、c2=a2+b2 | ||
| D、c=a+b |
如图，已知AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．不等式组
所表示的平面区域是面积为1的直角三角形，则z=x-2y的最大值是（ ）
|
| A、-5 | B、-2 | C、-1 | D、1 |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜