试编一个程序.计算全班物理考核学期总平均分.并给出流程图.其中考核占30%.期末考核占40%.平时占30%．——青夏教育精英家教网——

试编一个程序，计算全班物理考核学期总平均分，并给出流程图，其中考核占30%，期末考核占40%，平时占30%．

判断函数f（x）=

的单调性．

已知椭圆C：

=1（a＞b＞0），e=

，其中F是椭圆的右焦点，焦距为2，直线l与椭圆C交于点A、B，点A，B的中点横坐标为

（其中λ＞1）．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）求实数λ的值．

在平行四边形ABCD中，AC=

BD，则∠DAB的最大值为

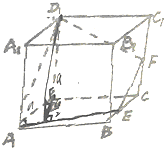
已知E、F分别为正方体ABCD-A₁B₁C₁D₁的棱BC，CC₁的中点，设α为二面角D-AE-D₁的平面角，求sinα=（　　）

已知定义在区间（0，+∞）上的函数f（x）满足f（

）=f（x₁）-f（x₂），且当x＞1时，f（x）＞0，求f（1），并判断f（x）的单调性．

已知点P圆C：（x-1）²+y²=2内的任意一点，直线l：x-y+b=0
（1）求点P在第一象限的概率；
（2）若b∈（-3，3），求直线l与圆C没有公共点的概率．

在平面直角坐标系xOy中，y轴正半轴上的点列{A_n}与曲线y=

（x＞0）上的点列{B_n}满足|OA_n|=|OB_n|=

，直线A_nB_n
在x轴上的截距为a_n，点B_n的横坐标为b_n，n∈N^*
（1）证明：a_n＞a_n+1＞4，n∈N^*
（2）证明：存在n₀∈N^*，使得对任意的n＞n₀，都有

已知f（x）是定义在R上的奇函数，当0≤x≤1时，f（x）=x²，当x＞0时，f（x+1）=f（x）+f（1），若直线y=kx与函数y=f（x）的图象恰有7个不同的公共点，则实数k的取值范围为（　　）

D、（4，8）

0 202194 202202 202208 202212 202218 202220 202224 202230 202232 202238 202244 202248 202250 202254 202260 202262 202268 202272 202274 202278 202280 202284 202286 202288 202289 202290 202292 202293 202294 202296 202298 202302 202304 202308 202310 202314 202320 202322 202328 202332 202334 202338 202344 202350 202352 202358 202362 202364 202370 202374 202380 202388 266669