题目内容
已知点P圆C:(x-1)2+y2=2内的任意一点,直线l:x-y+b=0
(1)求点P在第一象限的概率;
(2)若b∈(-3,3),求直线l与圆C没有公共点的概率.
(1)求点P在第一象限的概率;
(2)若b∈(-3,3),求直线l与圆C没有公共点的概率.
考点:几何概型
专题:概率与统计
分析:本题考查几何概型,解题的关键(1)是求解圆在第一象限的部分的面积,(2)直线l与圆C没有公共点的b的范围.然后由公式解之.
解答:
解:(1)如图:圆C:(x-1)2+y2=2,
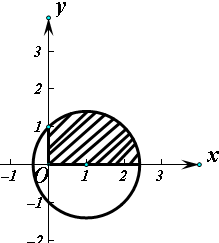
由几何概型的概率公式得,点P在第一象限的概率即圆在第一象限部分的面积与圆面积的比值:
=
.
所以点P在第一象限的概率为
;
(2)直线l与圆C没有公共点,则圆心(1,0)到直线l:x-y+b=0的距离为
>
,解得b>1或者b<-3,又b∈(-3,3),所以在此范围内直线l与圆C没有公共点的b∈(1,3),
所以由几何概型的概率公式得,b∈(-3,3),直线l与圆C没有公共点的概率
=
.
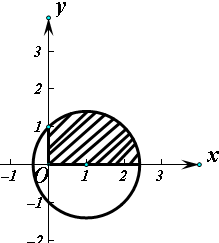
由几何概型的概率公式得,点P在第一象限的概率即圆在第一象限部分的面积与圆面积的比值:
| ||||
| 4π |
| 1+3π |
| 8π |
所以点P在第一象限的概率为
| 1+3π |
| 8π |
(2)直线l与圆C没有公共点,则圆心(1,0)到直线l:x-y+b=0的距离为
| |1+b| | ||
|
| 2 |
所以由几何概型的概率公式得,b∈(-3,3),直线l与圆C没有公共点的概率
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题考查了几何概型概率的求法,关键是明确满足条件的区域,是用长度还是面积或者体积表示,然后由概率公式解答.

练习册系列答案
相关题目
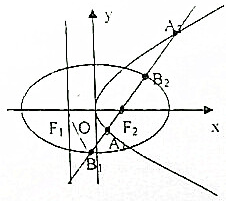 设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2,以F1、F2为焦点,离心率为
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2,以F1、F2为焦点,离心率为