题目内容
在平行四边形ABCD中,AC=
BD,则∠DAB的最大值为 .
| 3 |
考点:三角形中的几何计算
专题:计算题,解三角形
分析:由题意不妨设设AC、BD相交于点O,并设AO=CO=
,BO=DO=1,设AB=c,BC=b,从而利用余弦定理可得b2+c2=8,再利用余弦定理及基本不等式求最大值.
| 3 |
解答:
解:设AC、BD相交于点O,并设AO=CO=
,BO=DO=1,
设AB=c,BC=b,
则由余弦定理知:
cos∠AOB=
=
,
cos∠BOC=
,
而∠AOC+∠AOB=180°,
即有cos∠AOC=-cos∠AOB,
所以
=-
,
即有b2+c2=8;
从而在△ABD中再应用余弦定理知:
cos∠DAB=
=
;
而由8=b2+c2≥2bc知,
bc≤4;
所以cos∠ABC≥
;
由于∠DAB为锐角,
所以∠DAB≤60°
即知所以锐角DAB最大值为60°
故答案为60°.
| 3 |
设AB=c,BC=b,
则由余弦定理知:
cos∠AOB=
| 1+3-b2 | ||
2×1×
|
| 4-b2 | ||
2
|
cos∠BOC=
| 1+3-c2 | ||
2
|
而∠AOC+∠AOB=180°,
即有cos∠AOC=-cos∠AOB,
所以
| 4-b2 | ||
2
|
| 1+3-c2 | ||
2
|
即有b2+c2=8;
从而在△ABD中再应用余弦定理知:
cos∠DAB=
| b2+c2-4 |
| 2bc |
| 2 |
| bc |
而由8=b2+c2≥2bc知,
bc≤4;
所以cos∠ABC≥
| 1 |
| 2 |
由于∠DAB为锐角,
所以∠DAB≤60°
即知所以锐角DAB最大值为60°
故答案为60°.
点评:本题考查了解三角形的应用及基本不等式的应用,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知sin(
+α)=
,则cosα的值为( )
| 5π |
| 2 |
| 2 |
| 5 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、±
|
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,则实数k的取值范围为( )
A、(2
| ||||||
B、(
| ||||||
C、(2
| ||||||
| D、(4,8) |
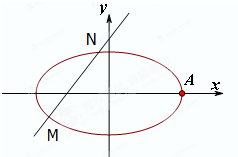 如图,已知点A是椭圆
如图,已知点A是椭圆
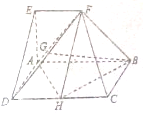 如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD
如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD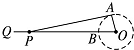 如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于
如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于