题目内容
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,则实数k的取值范围为( )
A、(2
| ||||||
B、(
| ||||||
C、(2
| ||||||
| D、(4,8) |
考点:函数奇偶性的性质,抽象函数及其应用
专题:函数的性质及应用
分析:本题通过奇函数特征得到函数图象经过原点,且关于原点对称,利用f(x+1)=f(x)+f(1)得到函数类似周期性特征,从而可以画出函数的草图,再利用两个临界状态的研究,得到k的取值范围.
解答:
解:∵当0≤x≤1时,f(x)=x2,
∴f(1)=1.
∵当x>0时,f(x+1)=f(x)+f(1),
∴f(x+1)=f(x)+1,
∴当x∈[n,n+1],n∈N*时,
f(x+1)=f(x-1)+1=f(x-2)+2=…=f(x-n)+n=(x-n)2+n,
∵函数f(x)是定义在R上的奇函数,
∴函数图象经过原点,且关于原点对称.
∵直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,
∴当x>0时,直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,
∴由x>0时f(x)的图象可知:
直线y=kx与函数y=f(x)的图象相切位置在x∈[1,2]时,直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,
直线y=kx与函数y=f(x)的图象相切位置在x∈[2,3]时,直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
∴直线y=kx与函数y=f(x)的图象位置情况介于上述两种情况之间.
∵当x∈[1,2]时,
由
得:
x2-(k+2)x+2=0,
令△=0,得:k=2
-2.
由
得:
x2-(k+4)x+6=0,
令△=0,得:k=2
-4.
∴k的取值范围为(2
-2,2
-4).

∴f(1)=1.
∵当x>0时,f(x+1)=f(x)+f(1),
∴f(x+1)=f(x)+1,
∴当x∈[n,n+1],n∈N*时,
f(x+1)=f(x-1)+1=f(x-2)+2=…=f(x-n)+n=(x-n)2+n,
∵函数f(x)是定义在R上的奇函数,
∴函数图象经过原点,且关于原点对称.
∵直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,
∴当x>0时,直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,
∴由x>0时f(x)的图象可知:
直线y=kx与函数y=f(x)的图象相切位置在x∈[1,2]时,直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,
直线y=kx与函数y=f(x)的图象相切位置在x∈[2,3]时,直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
∴直线y=kx与函数y=f(x)的图象位置情况介于上述两种情况之间.
∵当x∈[1,2]时,
由
|
x2-(k+2)x+2=0,
令△=0,得:k=2
| 2 |
由
|
x2-(k+4)x+6=0,
令△=0,得:k=2
| 6 |
∴k的取值范围为(2
| 2 |
| 6 |

点评:本题考查了函数的奇偶性、周期性、函数图象与性质及其应用,本题有一定的综合性,属于中档题.

练习册系列答案
相关题目
已知α为第四象限的角,且cos(
+α)=
则tanα=( )
| π |
| 2 |
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
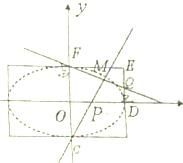 如图,在矩形ODEF中,O为坐标原点,|OD|=2,|DE|=
如图,在矩形ODEF中,O为坐标原点,|OD|=2,|DE|=