题目内容
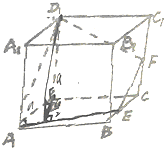 已知E、F分别为正方体ABCD-A1B1C1D1的棱BC,CC1的中点,设α为二面角D-AE-D1的平面角,求sinα=( )
已知E、F分别为正方体ABCD-A1B1C1D1的棱BC,CC1的中点,设α为二面角D-AE-D1的平面角,求sinα=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:二面角的平面角及求法
专题:空间角
分析:建立空间坐标系,求出平面AEFD1的法向量和平面AECD的一个法向量,代入向量夹角问题,是解答的关键.
解答:
解:建立如图所示的空间坐标系,
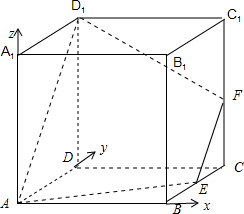
令正方体ABCD-A1B1C1D1的棱长为2,
则
=(2,1,0),
=(0,2,2),
设平面AEFD1的法向量为
=(x,y,z),
则由
得
,
令x=1,则y=-2,z=2,
故
=(1,-2,2),
又由
=(0,0,2)为平面AECD的一个法向量,α为D-AE-D的平面角,
∴cosα=
=
=
,
故sinα=
,
故选:B

令正方体ABCD-A1B1C1D1的棱长为2,
则
| AE |
| AD1 |
设平面AEFD1的法向量为
| m |
则由
|
|
令x=1,则y=-2,z=2,
故
| m |
又由
| AA1 |
∴cosα=
|
| ||||
|
|
| 4 |
| 3•2 |
| 2 |
| 3 |
故sinα=
| ||
| 3 |
故选:B
点评:本题考查的知识点是二面角的平面角及求法,建立空间坐标系,将二面角问题转化为向量夹角问题是解答的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
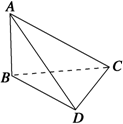 如图,在四面体ABCD中,AB=1,AD=2
如图,在四面体ABCD中,AB=1,AD=2| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
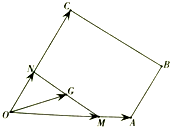 如图,梯形OABC中,OA=OC=2AB=1,OC∥AB,∠AOC=
如图,梯形OABC中,OA=OC=2AB=1,OC∥AB,∠AOC=