用数学归纳法证明“1+a+a2+…+an+1=
,(a≠1,n∈N*)”时,在验证n=1成立时,左边应该是( )
| 1-an+2 |
| 1-a |
| A、1+a+a2 |
| B、1+a+a2+a3 |
| C、1+a |
| D、1 |
数列{an}的通项公式为an=(-1)n+1•
,则a7=( )
| n+1 |
| n |
| A、8 | ||
B、-
| ||
C、
| ||
| D、7 |
若函数f(x)=
-
x2+x+1在区间(
,4)上有极值点,则实数a的取值范围是( )
| x3 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
A、(2,
| ||||
B、[2,
| ||||
C、(
| ||||
D、(2,
|
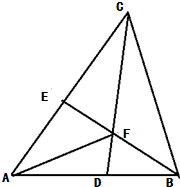 在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.
在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.